Ada banyak sekali jenis algoritma enkripsi yang ada, mulai dari yang paling sederhana sejak jaman kaisar Romawi Caesar, sampai yang paling modern dan canggih yang digunakan di sistem pertahanan negara. Namun pertanyaannya, adakah enkripsi yang tidak bisa dipecahkan, atau bahasa kerennya “unbreakable encryption” ?
Model Serangan (Attack Model)
Ada beberapa asumsi dalam model serangan dalam bahasan ini, kita asumsikan penyerang memiliki kemampuan di bawah ini:
- Mari kita asumsikan penyerang memiliki semua informasi tentang algoritma dan cara melakukan enkripsi dan dekripsi, artinya ini adalah algoritma terbuka, bukan algoritma yang rahasia.
- Kita juga asumsikan bahwa penyerang memiliki kekuatan komputasi yang tak terbatas, komputer super yang terkuat sejagat raya ada dalam genggamannya.
Dengan kemampuan seperti di atas, penyerang diberikan sebuah teks sandi (ciphertext), yang akan dipecahkan menjadi teks terang (plaintext).
Adakah algoritma enkripsi yang tidak mungkin dipecahkan dalam kerangka model serangan seperti di atas?
OTP (One-Time Pad)
Jawabannya ada, perkenalkan, One Time Pad. Ini adalah satu-satunya algoritma enkripsi yang secara matematis terbukti tidak mungkin dipecahkan, bahkan bila penyerang memiliki kemampuan komputasi tak terbatas sekalipun.
Sakti sekali bukan, mari kari kita bedah satu per satu kenapa OTP ini bisa sesakti ini.
Algoritma Sederhana Ekslusif-OR (XOR)
Algoritma OTP sangat sederhana, bisa diimplementasikan dengan menggunakan operasi XOR saja, jadi algoritma enkripsi dan algoritma dekripsi tidak ada bedanya, semua menggunakan operasi yang sama.
Kita bisa lihat dari tabel operasi XOR di level bit di tabel berikut ini.
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Dari tabel tersebut kita bisa melihat bahwa hasil operasi XOR bisa dikembalikan seperti semula dengan melakukan XOR yang sama sekali lagi.
Enkripsi: plaintext XOR kunci = ciphertext
Dekripsi: ciphertext XOR kunci = plaintext
Algoritma ini sangat sederhana, dalam python bisa diimplementasikan hanya dalam satu baris berikut:
"".join([chr(ord(a) ^ ord(b)) for a,b in zip(text_in,key)])Kenapa operasi sesederhana XOR bisa membuat algoritma yang tidak mungkin dipecahkan?
Kunci rahasia
Syarat utama operasi sesederhana XOR bisa menjadi algoritma enkripsi tak terkalahkan adalah penggunaan kunci rahasia yang acak sempurna (truly random), selain itu kunci harus memenuhi syarat-syarat berikut ini:
- Panjang kunci harus sama dengan panjang pesan, tidak boleh kurang satu bit pun karena setiap bit dari pesan akan di-XOR dengan setiap bit dari kunci.
- Kunci hanya boleh digunakan satu kali, kunci yang sama tidak boleh digunakan lagi untuk pesan yang lain. Maaf buat aktivis lingkungan, reuse and recycle kunci dilarang keras disini.
- Kunci harus acak sempurna (truly random). Ini sangat penting, kunci harus dibuat seacak mungkin dan tidak bisa ditebak. Bila kunci bisa ditebak, walau hanya sebagian saja, keamanan pesan akan terancam.
- Terakhir, tentu saja kuncinya harus benar-benar dijaga kerahasiaannya, kalau sampai bocor ya sudah selesai semua.
Dengan kunci semacam ini, walaupun penyerang mengetahui algoritma enkripsi/dekripsinya, penyerang tidak bisa mendapatkan plaintext sekalipun dengan kemampuan komputasi tak terbatas.
Mencoba semua kunci adalah sia-sia
Mencoba semua kemungkinan kunci adalah satu-satunya hal yang bisa dilakukan penyerang, dan itu tidak akan menghasilkan apa-apa.
Pertama, mencoba semua kemungkinan kunci membutuhkan waktu yang sangat lama. Sebuah pesan pendek 16 karakter string, semisal, “HALO APA KABARMU”, panjang kuncinya adalah 16×8 = 128 bit.
Ada sebanyak 2^128 kemungkinan kunci, yaitu 2 x 2 x 2 x 2 sebanyak 128 kali = 3.4028237 x 10^38, atau kurang lebih bisa ditulis sebagai “34” diikuti dengan 37 angka 0 dibelakangnya. Ini jumlah yang sangat besar, membutuhkan milyaran tahun untuk mencoba satu per satu semuanya. Ingat ini hanya untuk pesan sangat pendek 16 karakter.
Kedua, sesuai asumsi, penyerang memiliki kemampuan komputasi tak terbatas, anggaplah penyerang dapat mencoba semua kemungkinan kunci dalam waktu sangat singkat, tidak perlu milyaran tahun, penyerang tetap tidak akan mendapatkan pesan aslinya. Lho kok bisa?
Perhatikan kode python berikut ini. Pesan aslinya adalah “SERANG”, dengan kunci “XASDVF”, akan mengasilkan pesan sandi sebuah string ‘\x0b\x04\x01\x05\x18\x01’ sesuai tabel di bawah ini.
| Input | Kunci | input XOR kunci |
| ‘S’ | ‘X’ | \x0b |
| ‘E’ | ‘A’ | \x04 |
| ‘R’ | ‘S’ | \x01 |
| ‘A’ | ‘D’ | \x05 |
| ‘N’ | ‘V’ | \x18 |
| ‘G’ | ‘F’ | \x01 |
>>> text_in = "SERANG"
>>> key = "XASDVF"
>>> text_out = "".join([chr(ord(a) ^ ord(b)) for a,b in zip(text_in,key)])
>>> text_out
'\x0b\x04\x01\x05\x18\x01'Bila menggunakan kunci yang benar “XASDVF”, kita bisa mengembalikan teks sandi tersebut menjadi teks semula yaitu “SERANG”.
| Input | Kunci | input XOR kunci |
| \x0b | ‘X’ | ‘S’ |
| \x04 | ‘A’ | ‘E’ |
| \x01 | ‘S’ | ‘R’ |
| \x05 | ‘D’ | ‘A’ |
| \x18 | ‘V’ | ‘N’ |
| \x01 | ‘F’ | ‘G’ |
>>> text_in ='\x0b\x04\x01\x05\x18\x01'
>>> key = "XASDVF"
>>> text_out = "".join([chr(ord(a) ^ ord(b)) for a,b in zip(text_in,key)])
>>> text_out
'SERANG'Namun karena penyerang tidak mengetahui kunci yang benar, dia akan mencoba semua kemungkinan kunci, string 6 karakter. Perhatikan di bawah ini, penyerang mencoba dekripsi dengan kunci “FQOAMS”, ternyata menghasilkan pesan “MUNDUR”, padahal pesan aslinya adalah “SERANG”.
>>> text_in ='\x0b\x04\x01\x05\x18\x01'
>>> key = 'FQOAMS'
>>> text_out = "".join([chr(ord(a) ^ ord(b)) for a,b in zip(text_in,key)])
>>> text_out
'MUNDUR'Dengan kunci yang lain lagi “XM@BY0”, penyerang mendapatkan pesan yang berbeda yaitu “SIAGA1”.
>>> text_in ='\x0b\x04\x01\x05\x18\x01'
>>> key = 'XM@BY0'
>>> text_out = "".join([chr(ord(a) ^ ord(b)) for a,b in zip(text_in,key)])
>>> text_out
'SIAGA1'Anggaplah suatu saat setelah mencoba banyak kunci lainnya, dengan keberuntungan yang tinggi, penyerang mencoba kunci “XASDVF” (ini kunci yang benar), dan mendapatkan pesan “SERANG”.
Sampai disini penyerang mulai kebingungan, pesan aslinya “SERANG”, “MUNDUR” atau “SIAGA1” ?
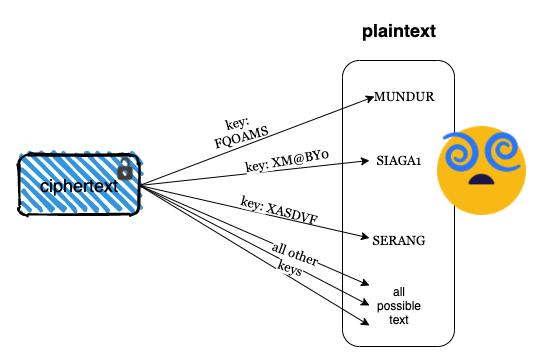
Kerahasiaan sempurna (perfect secrecy)
Penyerang memang bisa mencoba semua kemungkinan kunci, tapi setiap kemungkinan kunci itu akan menghasilkan pesan dekripsi yang berbeda-beda. Ini sama saja dengan penyerang menghasilkan pesan dekripsi dari semua kemungkinan string 6 karakter termasuk “MAKAN_”, “MINUM_”, “TIDUR_” dengan segala variasi huruf besar, huruf kecil, angka dan karakter khusus.
Penyerang tidak akan bisa mengetahui dengan pasti, dari semua string dekripsi tersebut, mana pesan aslinya, karena semua kemungkinan pesan dekripsi yang dihasilkan mempunyai peluang yang sama sebagai pesan yang asli. Kondisi inilah yang disebut dengan “perfect secrecy” oleh Claude Shannon, bapak teori informasi.
Jadi selama syarat-syarat kunci dipenuhi, OTP tidak mungkin dipecahkan. Penyerang hanya tahu panjang pesan saja, tidak mungkin mengetahui apa pesan aslinya, ini lah yang membuat OTP dijuluki sebagai “unbreakable encryption”.