XML Encryption adalah bagian dari standar xml security yang dibuat oleh W3C. XML encryption mendefinisikan standar bagaimana mengenkrip dokumen XML dengan granularitas tinggi, mulai dari mengenkrip seluruh dokumen XML atau hanya salah satu elemen saja dalam XML. Dalam tulisan ini saya akan membahas paper dari ilmuwan Jerman tahun 2011 berjudul “How to break XML encryption” yang memaparkan bagaimana memecahkan enkripsi XML encryption.
Teknik dekripsi XML encryption ini juga menggunakan “oracle” walaupun sedikit berbeda tetapi sangat disarankan untuk membaca dulu tulisan saya sebelumnya tentang padding oracle attack agar lebih mudah membaca tulisan ini karena beberapa konsep yang sudah dibahas disana tidak saya ulangi lagi disini.
XML Encryption
Cara untuk mengirimkan data yang terstruktur dari satu tempat ke tempat lain ada banyak cara, antara lain dengan JSON, YAML dan yang paling populer adalah XML. XML dipakai di banyak aplikasi, termasuk dalam aplikasi e-commerce dan web service sehingga kebutuhan untuk menjaga kerahasiaan data dalam XML sangat tinggi.
Bayangkan bila XML dipakai untuk mengirimkan purchase order seperti dibawah ini. Tentu sangat riskan bila data rahasia seperti kratu kredit dikirimkan apa adanya tanpa dilindungi kerahasiaannya dengan enkripsi.
Standar XML Encryption memiliki granularitas tinggi dalam hal data apa yang akan dienkripsi dalam XML. Kita bisa mengenkrip seluruh dokumen XML tersebut seperti dibawah ini.
Kita juga bisa hanya mengenkrip tag Payment dan semua sub-tagnya saja, sedangkan tag Order tidak dienkrip.
Bahkan bila data yang perlu dirahasiakan hanya data dalam tag CardId saja, sedangkan CardName, ValidDate tidak perlu dirahasiakan, itu juga bisa dilakukan dengan XML encryption.
Skema Padding XML Encryption
Soal padding sudah saya bahas panjang lebar di tulisan saya tentang padding oracle attack, dalam tulisan tersebut padding yang dipakai adalah standar PKCS#5 dan PKCS#7. XML encryption juga menggunakan padding untuk menggenapi plaintext menjadi berukuran tertentu sesuai dengan algoritma enkripsi yang dipakai seperti AES dengan blok berukuran 16 byte.
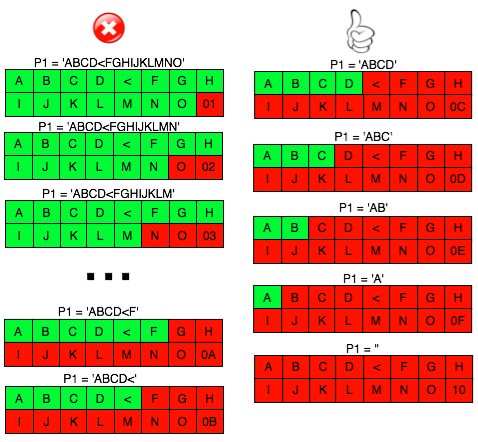
Padding pada standar XML Encryption berbeda dengan padding menurut aturan PKCS#5/#7. Byte terakhir menjadi petunjuk panjang padding byte, dalam hal ini masih sama dengan PKCS#5/#7. Namun bedanya dengan PKCS#5/#7, byte-byte yang menjadi padding pada standar XML encryption, boleh bernilai apapun, tidak harus bernilai sama dengan byte terakhir.
Sebagai contoh, bila byte terakhir bernilai 03, sesuai standar PKCS, 3 byte terakhir juga harus bernilai 03-03-03, sementara dalam standar XML encryption, 2 byte sebelum byte terakhir boleh bernilai apapun, tidak harus sama dengan byte terakhir.
Jadi padding XML encryption dikatakan valid bila byte terakhirnya bernilai antara 01-10 (bila satu blok berukuran 16 byte), tanpa perlu lagi melihat byte-byte sebelumnya seperti pada standar PKCS. Berikut adalah contoh-contoh padding yang valid.
AXIS sebagai “The Oracle”
Dalam tulisan ini kita menggunakan web service berbasis AXIS. Apache AXIS adalah salah satu implementasi dari protokol SOAP open source yang digunakan untuk web service.
Strategi attack ini adalah dengan mengirimkan “specially crafted”, ciphertext yang sudah kita susun sedemikian rupa sehingga ketika dikirimkan ke AXIS, dia akan meresponse dengan jawaban yes/no, valid/invalid yang bisa kita pakai untuk menebak-nebak hasil dekripsi ciphertext kita.
Sebelumnya kita harus mengenal dulu jenis respons yang diberikan oleh AXIS. Pertama adalah jenis error “security fault”, cirinya adalah jika kita menerima respons XML berikut ini.
Security fault bisa terjadi karena dua hal:
- Incorrect Padding
- Illegal XML Character (XML parsing failed)
Error ini terjadi bila byte terakhir bukan berada pada rentang 0x01-0x10 (1 byte s/d 16 byte).
Error ini terjadi bila blok berhasil didekrip (valid padding), namun plaintext hasil dekripsinya mengandung karakter yang tidak dibolehkan dalam XML atau mengandung kesalahan syntax XML. Karakter yang haram berada di XML adalah karakter dengan kode ASCII antara 00 – 1F kecuali karakter whitespace 09, 0A dan 0D.
Kesalahan sintaks XML mungkin terjadi bila hasil dekripsinya mengandung karakter 3C (“<") yang dianggap sebagai pembuka tag XML namun tidak diikuti dengan penutup tag yang benar, atau hasil dekripsinya mengandung karakter 26 ("&") sebagai pengawal entity tanpa diikuti dengan entity reference yang valid.
Kita tidak bisa membedakan apakah error security fault disebabkan karena incorrect padding atau invalid XML karena respons yang diterima sama. Jadi bila kita menerima security fault artinya ada kesalahan padding atau invalid XML.
Jenis respons berikutnya adalah application-specific error. Cirinya adalah ketika kita menerima respons seperti di bawah ini.
Jenis error ini terjadi setelah kita lolos dari jeratan security fault, artinya kita lolos dari kesalahan padding dan hasil dekripsinya pun tidak mengandung kesalahan XML. Namun karena kita tidak mengirimkan perintah web service yang benar, maka request kita dianggap salah.
Dari dua jenis respons ini kita bisa menyusun sebuah Oracle yang menjawab dengan jawaban boolean, yes/no. Bila kita mendapat respons security fault bisa kita anggap sebagai false, bila bukan security fault bisa dianggap sebagai true, atau sebaliknya.
Tergantung dari bagaimana kita menyusun pertanyaan dengan tepat, jawaban true/false dari “the oracle” bisa kita jadikan petunjuk untuk menebak-nebak plaintext hasil dekripsi ciphertext.
Byte Masking dalam CBC
Sedikit review mengenai mode CBC (cipher block chaining). Karena Pn = Cn-1 XOR Dec(Cn), maka bisa dikatakan isi Pn ditentukan oleh ciphertext blok sebelumnya.
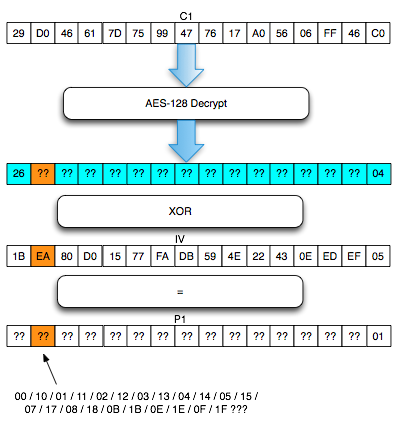
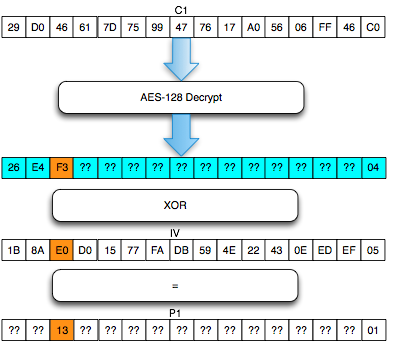
Perhatikan contoh pada gambar di bawah ini, P1 adalah IV XOR Dec(C1). Apa yang terjadi bila byte pertama IV kita XOR dengan A ? Bila byte pertama IV diXOR dengan A, yang terjadi adalah byte pertama P1 juga akan terXOR dengan A.
Jadi bila kita ingin mengubah P1, kita bisa lakukan dengan cara melakukan “masking”, yaitu mengXOR IV dengan byte masking tertentu, sehingga nilai P1 juga akan terXOR dengan byte yang sama. Prinsip ini sangat penting karena kita akan sering memainkan IV dengan cara meng-XOR IV pada posisi byte tertentu dengan suatu byte masking untuk membuat nilai P1 pada posisi tersebut terXOR juga.
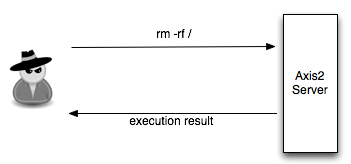
Remote Execution Web Service
Saya akan menjelaskan proses dekripsi ciphertext XML dengan contoh. Saya sudah menyiapkan web service yang melayani remote command execution di server Apache AXIS2. Web service ini menerima argument berupa command shell seperti ls, cat, uname dari client, kemudian mengirimkan hasil eksekusinya kepada client sebagai respons.
Berikut adalah hasil sniffing wireshark, contoh request dan respons, ketika client menginvoke service tersebut untuk mengeksekusi perintah “uname -v”.
Karena service remote command execution ini adalah service yang sangat sensitif, tentu saja harus dilindungi dari resiko berikut:
- Seorang peretas bisa mencuri dengar komunikasi antara client dan server
- Seorang peretas bisa mengirimkan command yang berbahaya seperti “rm -rf /” atau “shutdown -h now”
Secured Web Service
Sebagai jawaban dari ancaman resiko tersebut, web service tersebut akan dilindungi dengan xml encryption sehingga semua request dan response dari server dienkrip dengan symmetric encryption (dalam contoh ini digunakan AES-128 dalam mode CBC). Karena digunakan symmetric encryption, sebelumnya client dan server sudah sepakat dengan kunci rahasia yang akan digunakan untuk mengenkrip dan mendekrip request dan response.
Dengan xml encryption walaupun si peretas tetap bisa menyadap komunikasi client dan server namun kini dia tidak bisa lagi mengerti apa isi komunikasinya.
Si peretas juga tidak bisa mengirimkan malicious command lagi karena dia harus mengirimkan command tersebut dalam bentuk encrypted sedangkan dia tidak tahu kunci untuk mengenkripnya. Tanpa kunci yang benar, command yang dia kirim ke server ketika didekrip di server akan menjadi “garbage text” yang jelas akan ditolak server.
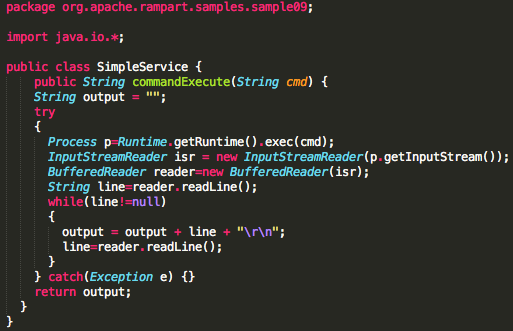
Berikut adalah source code web service yang sudah diamankan dengan xml encryption. Saya mengambil dan memodifikasi sedikit dari sample #09 yang dibawa oleh rampart 1.5. Pada intinya source code tersebut menerima input String cmd kemudian memanggil Runtime.exec() untuk mengeksekusi command shell.
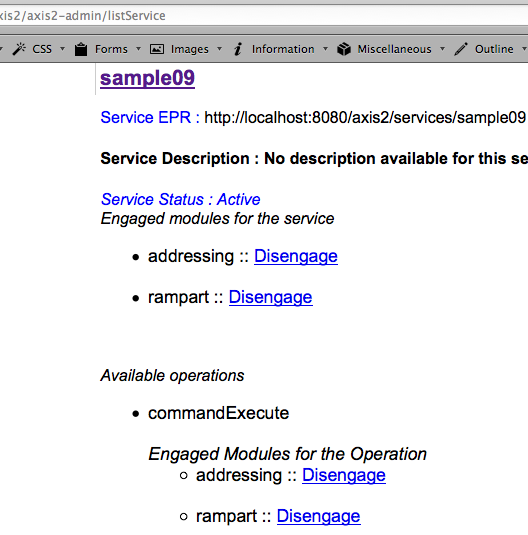
Web service tersebut saya compile dan deploy dalam Apache Tomcat 5.5.36 + Axis2 1.5.3 + Rampart 1.5. Versi Axis2 dan rampart sengaja saya pilih versi yang masih vulnerable terhadap serangan ini.
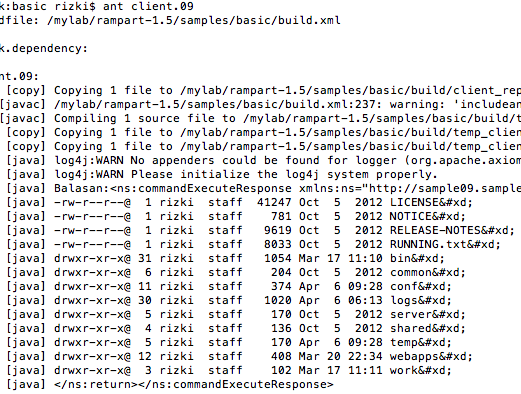
Gambar berikut memperlihatkan contoh ketika seorang client menginvoke web service ‘commandExecute’ dengan input parameter “ls -l”.
Dengan melakukan sniffing peretas memang masih bisa mendapatkan komunikasi web service antara client dan server. Namun karena web service ini sudah diamankan dengan xml encryption, maka dia hanya mendapatkan request dan respons dalam bentuk ciphertext saja.
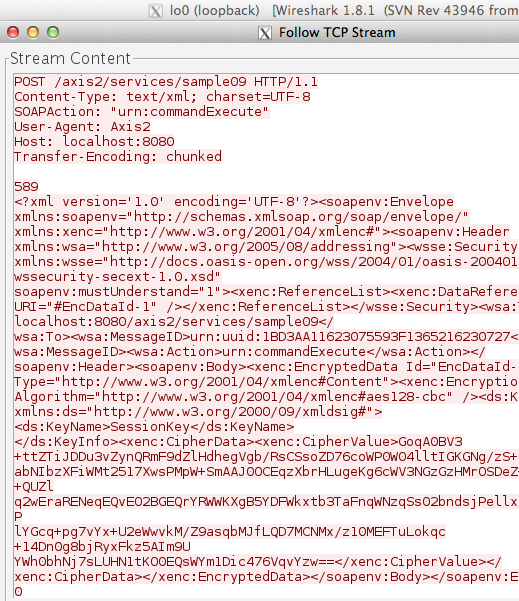
Gambar di bawah ini request POST dari client ke server yang didapatkan dari hasil sniffing dengan wireshark.
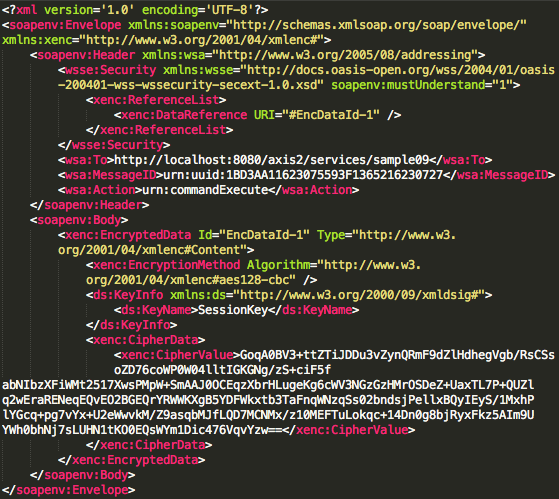
Dari request POST tersebut SOAP message yang dikirim client terlihat pada gambar di bawah ini. SOAP message ini meng-invoke service “commandExecute” dengan input berupa command shell. Namun berbeda dengan hasil sniffing pada web service yang tidak diamankan dengan xml encryption, kali ini command shell yang dieksekusi tidak terlihat karena sudah dalam bentuk terenkripsi.
Pada tag EncryptionMethod atribut algorithm menunjukkan bahwa enkripsi yang dipakai adalah AES dengan panjang blok 128 bit dan dalam mode CBC (cipher block chaining). Kalau peretas ingin mengetahui command shell apa yang dikirim ke server dia harus mendekrip ciphertext yang tersimpan pada tag CipherValue dalam bentuk base64 encoded.
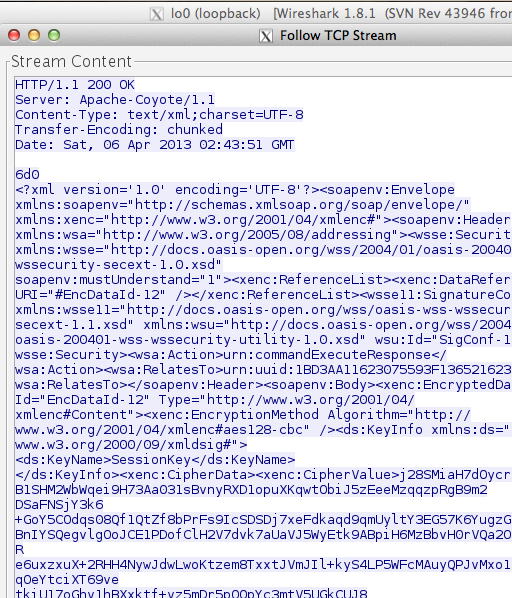
Sedangkan gambar di bawah ini adalah response dari server ke client yang didapatkan dari hasil sniffing dengan wireshark.
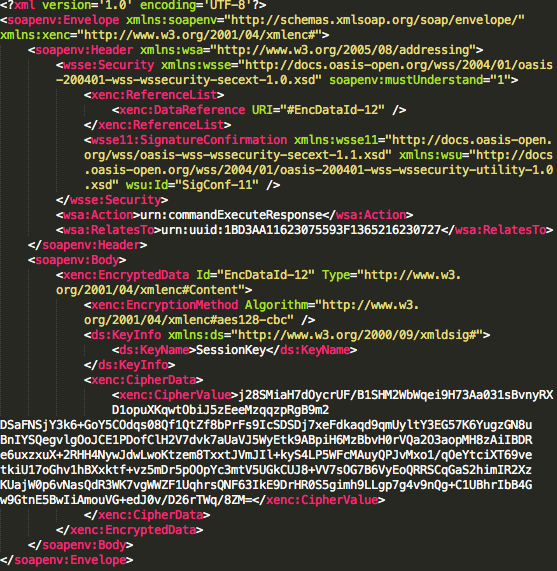
Dari hasil sniffing tersebut SOAP message response dari server terlihat pada gambar di bawah ini. Hasil eksekusi command juga tidak bisa dilihat karena sudah terenkrip. Kalau peretas ingin mengetahui hasil eksekusi command dari client, dia harus mendekrip ciphertext yang ada pada tag CipherValue dalam bentuk base64 encoded.
Hollywoord Style Decryption
Apakah benar dengan menggunakan XML Encryption masalah akan selesai? Peretas tidak bisa membaca komunikasi antara client dan server dan tidak bisa juga mengirimkan malicious command?
Ternyata si peretas masih bisa mendekrip komunikasi terenkrip antara client dan server walaupun tidak mengetahui kuncinya, dia juga bisa mengirimkan malicious command ke server sekali lagi tanpa mengetahui kuncinya.
Mirip dengan padding oracle attack, kita akan memanfaatkan AXIS2 server sebagai “the oracle” untuk membantu kita mendekrip ciphertext (dan juga mengenkrip ciphertext) byte per byte. Cara dekripsi ciphertext byte per byte ini sering terlihat di film-film hollywood.
Saya telah membuat tools untuk melakukan dekripsi ciphertext baik dari sisi client (request) maupun dari sisi server (response). Berikut adalah rekaman screen recording ketika tools tersebut dijalankan.
Source code dari tools di atas: source code.
Bagaimana cara kerja tools di atas? Bagaimana kita bisa memanfaatkan AXIS2 server sebagai “the oracle” untuk mendekrip ciphertext? Silakan ikuti penjelasannya di bawah ini.
Decrypting Request
Kita bisa mendekrip ciphertext request dari client maupun ciphertext response dari server. Mari kita mulai dengan mendekrip ciphertext request dari client. Berikut adalah ciphertext yang harus didekrip oleh si peretas.
Ciphertext di atas adalah dalam bentuk base64 encoded yang terbagi menjadi blok-blok seukuran 16 byte (128 bit). Blok ciphertext pertama (16 byte pertama) adalah initialization vector (IV). Ciphertext tersebut di atas terdiri dari satu blok IV dan 15 blok ciphertext seperti pada gambar di bawah ini.
Kita akan mendekrip satu blok per satu blok dimulai dari blok ciphertext pertama (C1).
Find IV Procedure
Karena kita akan mendekrip C1, maka kita akan menggunakan dua blok, C0 sebagai IV dan C1 sebagai blok ciphertext target yang akan didekrip. Begitu juga nanti bila kita akan mendekrip blok C2, maka blok yang digunakan adalah C1 sebagai IV dan C2 sebagai blok target.
Ketika mendekrip selalu digunakan sepasang blok, blok pertama sebagai IV dan blok kedua sebagai ciphertext target yang akan didekrip. Blok kedua selalu tetap, sedangkan blok pertama (IV) adalah blok yang berubah-ubah, dimanipulasi untuk mengorek informasi dari “The Oracle”
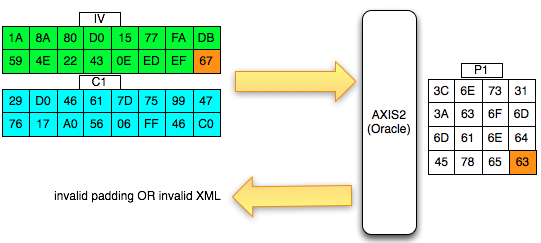
Kalau kita potong ciphertextnya hanya dua blok awal saja kemudian kita kirimkan ke AXIS2 server, maka kita akan mendapat response error invalid padding karena byte terakhir dari blok pertama kini dianggap byte yang menunjukkan panjang padding (panjang padding yang valid antara 1-16 byte). Jadi bila hasil dekrip byte terakhir blok pertama tersebut nilainya bukan antara 0x01 – 0x10 maka akan menghasilkan error, invalid padding.
Pada gambar di bawah ini terlihat bahwa di server byte terakhir hasil dekripnya IV+C1 (P1) adalah 0x63 sehingga jelas bukan padding yang valid. Server AXIS2 akan memberikan response “invalid padding OR invalid XML” dalam bentuk error “security fault” (karena error messagenya sama, kita tidak bisa membedakan apakah security fault disebabkan karena invalid padding atau invalid XML).
Dalam hal ini seperti tulisan sebelumnya tentang padding oracle, server AXIS2 bertindak sebagai ‘the oracle’ yang bisa kita interogasi untuk mendekrip ciphertext.
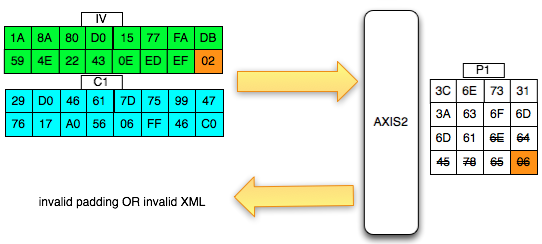
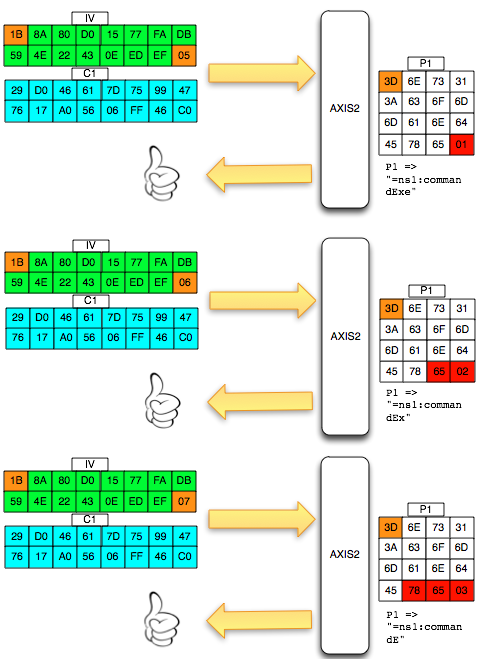
Agar kita mendapatkan hasil dekrip dengan padding byte yang valid (antara 0x01-0x10), kita harus mencari byte terakhir IV yang membuat byte terakhir P1 valid. Gambar di bawah ini menunjukkan ketika byte terakhir IV bernilai 0x02, maka byte terakhir P1 bernilai 06 yang berarti valid padding.
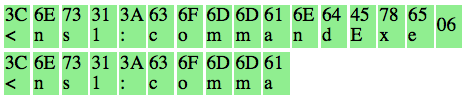
Walaupun kita sudah temukan IV yang membuat P1 valid padding, namun kita tetap mendapatkan error “invalid padding OR invalid XML” kenapa begitu ? Mari kita lihat isi dari P1 pada gambar di bawah ini. Setelah 6 byte terakhir dibuang, hasil akhirnya adalah teks: “<nsl:comma” yang jelas bukan XML yang valid karena ada karakter pembuka tag 3C (“<“) yang tidak ditutup.
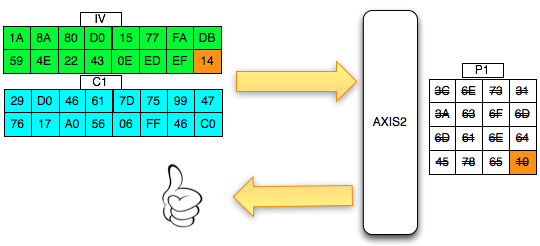
Karena ada karater pembuka tag “<” di awal blok maka satu-satunya yang bisa membuat P1 tidak mendapatkan error “invalid padding dan invalid XML” adalah ketika byte terakhir P1 bernilai 10 hexa (16 byte). Dengan byte terakhir bernilai 10 hexa (16 byte), artinya semua isi P1 akan dibuang karena dianggap byte padding, dengan kata lain P1 akan menjadi empty string. Karena P1 adalah empty string, maka lolos dari jeratan error “invalid padding” dan “invalid XML”.
Bila dalam blok tersebut tidak ada karakter 3C (“<“), maka kita akan mendapatkan 16 IV yang menghasilkan valid padding dan valid XML. Bila jumlah IV yang membuat valid padding dan valid XML tidak mencapai 16, artinya dalam plaintextnya mengandung karakter “<” di posisi “jumlah IV”:
- Bila jumlah IV yang valid hanya satu, artinya di byte ke-1 ada karakter “<” dan byte padding yang valid adalah 10 hexa.
- Bila jumlah IV yang valid ada 2, artinya di byte ke-2 ada karakter “<” dan byte padding yang valid adalah 0F dan 10 hexa.
- Bila jumlah IV yang valid ada 3, artinya di byte ke-3 ada karakter “<” dan byte padding yang valid adalah 0E, 0F dan 10.
- Bila jumlah IV yang valid ada 4, artinya di byte ke-4 ada karakter “<” dan byte padding yang valid adalah 0D, 0E, 0F dan 10.
- Bila jumlah IV yang valid ada 5, artinya di byte ke-5 ada karakter “<” dan byte padding yang valid adalah 0C, 0D, 0E, 0F dan 10
- dan seterusnya
Contoh dalam gambar di bawah ini menunjukkan bahwa dari 16 byte padding yang valid, hanya ada 5 yang menghasilkan P1 yang valid. Sisanya 11 byte padding dari 01-0B masih menyisakan karakter “<” sehingga hasil akhirnya menjadi invalid XML. Begitu si peretas mendeteksi ada 5 IV yang valid, maka bisa diketahui bahwa di karakter ke-5 mengandung karakter “<“.
Jumlah IV yang valid menunjukkan posisi karakter “<“
Kembali lagi ke contoh kita. Setelah kita mencoba semua kemungkinan byte terakhir IV dari 0-255, kita hanya mendapatkan satu IV yang tidak menghasilkan respons invalid padding dan invalid XML. Dari hasil ini kita meyakini bahwa karakter pertama P1 adalah “<” (0x3C).
Mengubah “<” menjadi “=”
Oke, kini kita sudah berhasil mendapatkan satu byte pertama, yaitu karakter “<“. Lalu apa lagi ? Sebenarnya yang ingin kita dapatkan di tahap “Find IV” ini adalah mendapatkan 16 IV yang tidak menghasilkan respons invalid padding dan invalid XML. Tapi karena ada karakter “<” di byte pertama, kita hanya mendapatkan 1 saja.
Agar kita bisa mendapatkan 16 IV yang valid, kita harus menghilangkan karakter “<” dengan mengubahnya menjadi karakter “=”. Bagaimana caranya? Itu mudah, kita sudah tahu posisi karakter “<” di byte ke berapa, selanjutnya kita hanya perlu menyesuaikan IV di byte tersebut agar P1 di posisi tersebut berubah dari “<” menjadi “=”.
Bagi yang sudah membaca padding oracle di tulisan saya sebelumnya tentu mengerti caranya, yaitu dengan operasi XOR karena dalam mode CBC, P1 adalah hasil XOR antara IV dan hasil dekrip C1, dengan memainkan IV kita bisa menentukan P1 mau dibuat menjadi apa. Karena 3C (“<“) XOR 3D (“=”) adalah 01, maka IV di posisi yang mengandung karakter 3C harus kita XOR-kan 01 agar hasil akhirnya nanti byte pertama P1 berubah menjadi “=”.
Kita tadi menggunakan IV dengan byte pertama 1A, setelah kita XOR dengan 01, maka kini byte pertama IV kita menjadi 1B. Dengan byte pertama IV 1B, maka byte pertama P1 dijamin bernilai “=” bukan lagi “<“.
Setelah kita mem-fix-kan byte pertama P1 menjadi “=”, kita harus mengulangi lagi prosedur find IV sampai kita mendapatkan 16 IV yang valid. Gambar di bawah ini menunjukkan 3 IV yang menghasilkan valid P1 setelah byte pertama P1 dikunci menjadi “=”. Perhatikan bahwa byte pertama IV sudah kita tetapkan 1B sehingga byte pertama P1 selalu bernilai 3D (“=”).
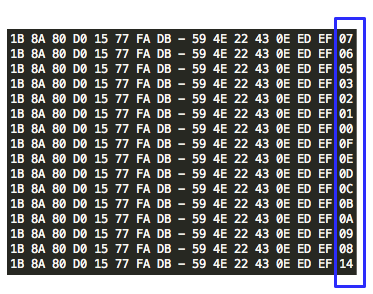
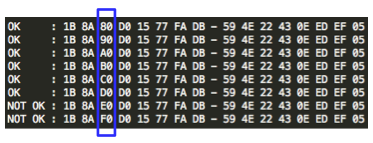
Bila proses ini diteruskan, kita akan menemukan 16 IV yang membuat P1 menjadi valid. Gambar berikut adalah daftar 16 IV yang menghasilkan P1 yang valid. Perhatikan bahwa hanya byte terakhir saja yang berbeda dan byte pertama selalu 1B.
Sampai sini kita hanya mengumpulkan 16 IV yang menghasilkan byte terakhir P1 yang valid antara 01-10 hexa. Kita tidak tahu IV mana yang menghasilkan byte terakhir 01. Kita hanya menginterogasi AXIS2 sebagai “the oracle” dan the oracle hanya menjawab valid atau tidak valid, dia tidak pernah memberitahukan isi P1.
Namun ada sedikit petunjuk yang bisa kita pakai, dari ke-16 byte terakhir IV tersebut, hanya ada satu yang bit ke-4nya berbeda dari yang lain. IV yang berbeda sendiri itu adalah IV yang membuat P1 berakhiran 10 hexa. Hanya itu petunjuk yang kita tahu. Kita hanya bisa mencari IV mana yang membuat P1 menjadi berakhiran dengan byte 10 hexa.
Secara sepintas sebenarnya sudah bisa dilihat, 15 IV yang lain depannya adalah 0, sedangkan hanya dia sendiri yang depannya adalah 1, jadi bisa disimpulkan bahwa IV dengan byte terakhir 14 hexa adalah IV yang membuat byte terakhir P1 menjadi 10 hexa.
Membuat Single Byte Padding
Sebenarnya tujuan akhir pada fase “find IV” ini adalah kita mencari IV yang membuat P1 menjadi berakhiran dengan byte 01 (single byte padding). Kita telah mengetahui bahwa byte terakhir IV 14 menghasilkan byte terakhir P1 10. Berapakah byte terakhir IV yang membuat byte terakhir P1 menjadi 01 ?
Dengan operasi matematika sederhana bisa kita hitung, 10 XOR 01 = 11, sehingga 14 XOR 11 = 05. Jadi sekarang kita sudah mendapatkan informasi bahwa byte terakhir IV 05 menghasilkan byte terakhir P1 01. Kok bisa begitu? Tentu saja bisa, just simple math 🙂 Bila anda masih bingung, silakan baca lagi tulisan saya tentang “Padding Oracle Attack” yang menjelaskan tentang operasi XOR pada block cipher mode CBC.
Jadi prosedur Find IV ini diakhiri dengan didapatkannya IV berikut ini:
Dengan IV tersebut, dijamin P1 akan berakhiran dengan 01 (single byte padding).
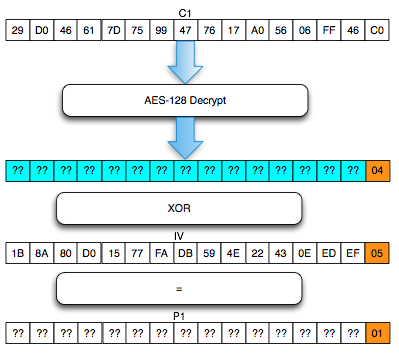
Mencari byte terakhir
Hal paling mudah yang bisa kita lakukan di tahap ini adalah mencari byte terakhir hasil dekrip C1. Sebelumnya kita sudah tahu bahwa dengan IV yang berakhiran 05, maka byte terakhir P1 adalah 01. Dari sini bisa kita ketahui bahwa byte terakhir hasil dekrip C1 adalah 05 XOR 01 = 04.
Masih ada 15 byte lain hasil dekrip C1 yang belum diketahui. Mari kita lanjutkan prosesnya untuk mencari byte ke-1 sampai byte ke-15.
Mencari Byte ke-1
Kita mulai dari mencari byte pertama dulu baru kemudian mencari byte berikutnya sampai byte ke-15.
Strategi mencari byte ke-X adalah dengan menggunakan IV yang sudah kita temukan dalam prosedur “Find IV” sebagai IV dasar. IV tersebut akan kita ubah pada posisi byte ke-X kemudian mengamati respons dari “the oracle” AXIS2 Server, apakah perubahan IV pada byte ke-X tersebut mentrigger error ?
Bila ternyata setelah IV diubah di posisi byte ke-X terjadi error, maka bisa dipastikan error tersebut karena adanya “illegal character” di posisi byte ke-X (tidak mungkin karena invalid padding karena IV tersebut sudah kita kunci agar paddingnya selalu 01). Response dari “the oracle” tersebut bisa kita gunakan untuk menebak hasil dekripsi C1.
Jadi pertama yang akan kita lakukan adalah mencari byte pertama IV yang membuat “the oracle” memberikan response error invalid XML. Kita akan mencari byte pertama IV tersebut dengan melakukan XOR antara byte pertama IV dasar kita dengan byte 0x00, 0x10, 0x20, 0x30, 0x40, 0x50, 0x60 dan 0x70 dan mencatat IV mana saja yang menghasilkan error “invalid XML”.
Kita akan menginterogasi “the oracle” untuk menjawab pertanyaan-pertanyaan:
- Apakah dengan byte pertama IV 1B XOR 00 = 1B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 10 = 0B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 20 = 3B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 30 = 2B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 40 = 5B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 50 = 4B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 60 = 7B, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 1B XOR 70 = 6B, menghasilkan error invalid XML ?
Ternyata setelah dicoba, didapatkan hasil bahwa hanya ada satu IV yang membuat error invalid XML, yaitu bila byte pertama IV bernilai 3B (=1B XOR 20).
Bila hanya ada satu IV yang membuat jadi invalid XML, maka kemungkinan byte pertama P1 adalah 19, 1A atau 1D. Kita belum tahu yang mana, yang jelas di antara tiga itu. Kita perlu menginterogasi “the oracle” lebih lanjut untuk mendapatkan konfirmasi lanjutan apakah 19, 1A atau 1D.
Sebagai cara untuk konfirmasi, kita akan membuat tiga kandidat P1 (19 / 1A / 1D) menjadi byte 3C “<” sehingga men-trigger error invalid XML. Kita akan malakukan byte masking sekali lagi dengan byte 25, 26, 21 karena 19 XOR 25 = 3C, 1A XOR 26 = 3C dan 1D XOR 21 = 3C.
Ingat bila IV di XOR dengan A, maka P1 juga akan berubah menjadi P1 XOR A.
Byte pertama IV (3B) akan kita XOR dengan 25, 26 dan 21 kemudian kita interogasi “the oracle” untuk mengetahui jawaban pertanyaan berikut:
- Apakah dengan byte pertama IV 3B XOR 25 = 1E, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 3B XOR 26 = 1D, menghasilkan error invalid XML ?
- Apakah dengan byte pertama IV 3B XOR 21 = 1A, menghasilkan error invalid XML ?
Setelah dicoba, hanya 1A (=3B XOR 21) yang menghasilkan error invalid XML. Perhatikan bahwa ketika byte pertama IV di-XOR dengan 21, maka byte pertama P1 juga akan ter-XOR dengan 21. Karena byte pertama P1 diXOR 21 mentrigger error invalid XML, maka diyakini bahwa byte pertama P1 XOR 21 = 3C sehingga kita dapat konfirmasi kepastian bahwa byte pertama P1 adalah 1D.
Dengan mengetahui byte pertama IV dan byte pertama P1, kita bisa menghitung byte pertama hasil dekrip C1 adalah 3B XOR 1D = 26 atau bisa juga menggunakan 1A XOR 3C = 26.
Mencari Byte ke-2
Mari kita lanjutkan untuk mencari byte ke-2, masih dengan menggunakan IV dasar hasil prosedur “Find IV” yang membuat single byte padding. Dengan prosedur yang sama kita harus mengubah byte ke-2 IV tersebut sehingga mentrigger error invalid XML.
Sama seperti cara mencari byte pertama, kali ini byte ke-2 IV akan kita XOR-kan dengan byte 00,10,20,30,40,50,60,70 sehingga byte ke-2 P1 juga akan ter-XOR dengan byte-byte tersebut. Dari ketujuh byte mask 00 – 70 tersebut akan ada satu atau lebih yang membuat P1 berubah menjadi karakter illegal sehingga mentrigger error invalid XML.
Sekali lagi kita akan menginterogasi “the oracle” untuk menjawab pertanyaan-pertanyaan:
- Apakah dengan byte ke-2 IV 8A (=8A XOR 00), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV 9A (=8A XOR 10), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV AA (=8A XOR 20), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV BA (=8A XOR 30), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV CA (=8A XOR 40), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV DA (=8A XOR 50), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV EA (=8A XOR 60), menghasilkan error invalid XML ?
- Apakah dengan byte ke-2 IV FA (=8A XOR 70), menghasilkan error invalid XML ?
Setelah dicoba kali ini sedikit berbeda, ada lebih dari satu IV yang mentrigger error invalid XML, yaitu EA dan FA. Pasangan IV tersebut tersebut membuat P1 menjadi pasangan “illegal XML character” berikut:
- 0x00 dan 0x10
- 0x01 dan 0x11
- 0x02 dan 0x12
- 0x03 dan 0x13
- 0x04 dan 0x14
- 0x05 dan 0x15
- 0x07 dan 0x17
- 0x08 dan 0x18
- 0x0B dan 0x1B
- 0x0E dan 0x1E
- 0x0F dan 0x1F
Kita tidak tahu, EA dan FA membuat P1 menjadi pasangan yang mana? Oleh karena itu kita butuh konfirmasi lebih lanjut dari “the oracle” untuk memastikan. Sebenarnya kita tidak perlu menguji kedua IV tersebut karena yang manapun yang kita pilih hasilnya akan sama, jadi kita pilih salah satu saja yang pertama, EA.
Sampai disini kita tidak tahu, byte ke-2 IV EA membuat byte ke-2 P1 menjadi bernilai berapa? Kita hanya tahu byte ke-2 P1 adalah salah satu dari 22 kandidat: 00, 10, 01, 11, 02, 12, 03, 13, … ,0E, 1E, 0F, 1F.
Lagi-lagi kita gunakan byte mask untuk menguji kandidat. Karena kita ingin membuat byte ke-2 P1 bernilai 3C, maka semua 22 kemungkinan P1 tersebut kita XOR dengan 3C untuk membuat 22 byte mask. Jadi byte mask yang akan kita pakai untuk menguji adalah:
- 0x3C (=00 XOR 3C)
- 0x2C (=10 XOR 3C)
- 0x3D (=01 XOR 3C)
- 0x2D (=11 XOR 3C)
- 0x3E (=02 XOR 3C)
- 0x2E (=12 XOR 3C)
- 0x3F (=03 XOR 3C)
- 0x2F (=13 XOR 3C)
- dan seterusnya.. 0x38, 0x28, 0x39, 0x29, 0x3B, 0x2B, 0x34, 0x24, 0x37, 0x27, 0x32…
- 0x22 (=1E XOR 3C)
- 0x33 (=0F XOR 3C)
- 0x23 (=1F XOR 3C)
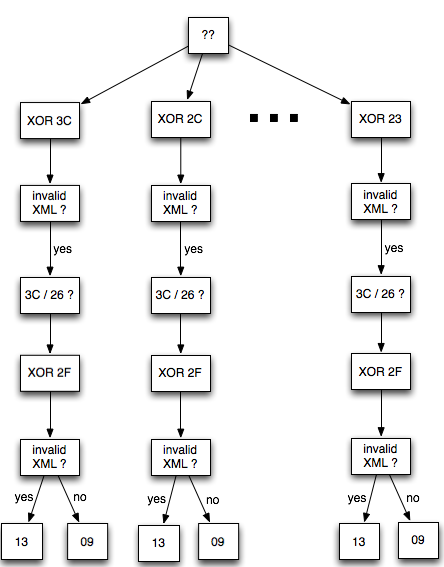
Gambar berikut menunjukkan alur logika bagaimana dengan jawaban valid/invalid XML dari “the oracle” kita bisa menebak dengan tepat isi byte ke-2 P1.
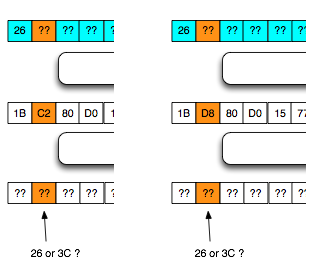
Setelah IV 0xEA di XOR dengan 22 byte mask di atas ditemukan dua di antaranya yang mentrigger error invalid XML, yaitu C2 (=EA XOR 28) dan D8 (=EA XOR 32).
Karena kandidatnya tinggal dua kemungkinan, 26 atau 3C dan diketahui bahwa 26 XOR 2F = 09 (karakter legal, tidak mentrigger error invalid XML) sedangkan 3C XOR 2F = 13 (karakter ilegal, mentrigger invalid XML), maka kita akan gunakan byte mask 0x2F sebagai pembeda di antara keduanya.
Sekali lagi kita tidak perlu memakai kedua IV tersebut, cukup gunakan salah satu saja, C2 atau D8, yang manapun yang dipilih hasilnya sama saja. Dalam contoh ini kita pilih saja C2 sebagai byte ke-2 IV.
Ingat, bila IV diXOR dengan 2F, maka P1 nilainya juga akan berubah menjadi P1 XOR 2F
Kita akan menginterogasi “the oracle” untuk mengetahui jawaban dari pertanyaan:
- Apakah dengan mengubah byte ke-2 IV menjadi ED (=C2 XOR 2F), akan mentrigger error invalid XML ?
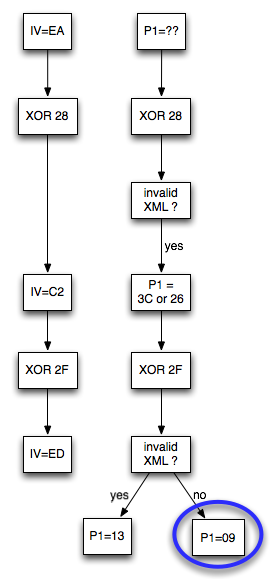
Bila jawaban dari AXIS “the oracle” adalah no (tidak mentrigger error invalid XML), maka bisa dipastikan bahwa byte ke-2 P1 adalah 09. Sebaliknya bila jawaban “the oracle” adalah yes, maka bisa dipastikan bahwa byte ke-2 P1 adalah 13.
Setelah dicoba dengan megubah byte ke-2 IV menjadi ED ternyata tidak mentrigger error invalid XML, sehingga kita yakin bahwa byte ke-2 P1 adalah 09. Dengan mengetahui byte ke-2 IV dan byte ke-2 P1, maka kita bisa menghitung byte ke-2 hasil dekrip C1 adalah ED XOR 09 = E4.
Mencari Byte ke-3
Sejauh ini kita sudah mendapatkan 3 byte, yaitu byte ke-1, ke-2 dan byte terakhir. Kini kita lanjutkan pencarian kita untuk mencari byte ke-3.
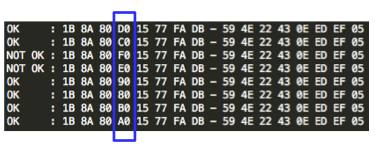
Karena yang dicari adalah byte ke-3, maka kita akan mengXORkan byte ke-3 IV 80 dengan byte mask 00, 10, 20 – 70 kemudian mencatat byte mask mana yang mentrigger error invalid XML. Gambar di bawah ini memperlihatkan proses mencari byte ke-3 IV yang mentrigger error invalid XML.
Setelah dicoba diketahui bila byte ke-3 IV bernilai E0 (=80 XOR 60) atau F0 (=80 XOR 70) mentrigger error invalid XML. Dalam contoh ini kita ambil salah satu saja, yaitu E0.
Selanjutnya byte ke-3 IV, E0 akan diubah dengan meng-XOR-kan dengan 22 byte mask (yang sudah dijelaskan sebelumnya ketika mencari byte ke-2) untuk mencari mencari lagi mana di antara 22 byte ke-3 IV tersebut yang mentrigger error invalid XML.
Gambar di bawah ini menunjukkan proses interogasi “the oracle” untuk byte ke-3 IV yang berbeda-beda (XOR dengan 22 byte masking). Ternyata baru pada percobaan ke-8, sudah ditemukan byte ke-3 IV yang mentrigger error invalid XML, yaitu CF (=E0 XOR 2F).
Seperti yang sudah dijelaskan sebelumnya, byte ke-3 IV CF ini membuat byte ke-3 P1 menjadi dua kemungkinan, 3C atau 26. Untuk memastikan byte ke-3 P1 adalah 3C atau 26 kita harus menginterogasi “the oracle” lagi. Byte ke-3 IV, CF kita XOR dengan 2F (akibatnya byte ke-3 P1 juga akan ter-XOR dengan 2F) kemudian kita lihat respons dari “the oracle”, apakah mentrigger error invalid XML lagi atau tidak. Bila the oracle merespons dengan error invalid XML, artinya byte ke-3 P1 adalah 13, bila the oracle tidak merespons dengan “invalid xml”, maka byte ke-3 P1 adalah 09.
Ternyata setelah byte ke-3 IV (CF) di-XOR dengan 2F menjadi E0, mentrigger error invalid XML, sehingga kita yakin bahwa byte ke-3 IV tersebut (E0) membuat byte ke-3 P1 menjadi 13. Dengan mengetahui byte ke-3 IV E0 dan byte ke-3 P1 13, kita bisa menghitung byte ke-3 hasil dekrip C1 yaitu E0 XOR 13 = F3.
Mencari byte ke-4
Mari kita lanjutkan untuk mencari byte ke-4. Karena yang dicari adalah byte ke-4, maka byte ke-4 IV (D0) di XOR dengan 7 byte masking (00-10-20-30…-70) untuk mencari byte ke-4 IV yang mentrigger error invalid XML. Berikut adalah proses mencari byte ke-4 IV yang menghasilkan error invalid xml.
Dari gambar di atas terlihat bahwa byte ke-4 IV F0 dan E0 mentrigger error invalid XML. Karena ada dua IV kita pilih saja yang pertama, yaitu F0. Selanjutnya prosesnya sama, kita mengXORkan F0 dengan 22 byte masking untuk mencari byte masking yang mentrigger error invalid XML.
Gambar di atas menunjukkan bahwa ketika byte ke-4 IV bernilai DD (=F0 XOR 2D) membuat “the oracle” merespons dengan error invalid XML. Selanjutnya diperlukan konfirmasi sekali lagi dari the oracle untuk menentukan nilai byte ke-4 P1.
Byte ke-4 IV DD diXORkan dengan 2F menjadi F2 kemudian kita amati respons dari “the oracle”. Ternyata respons dari “the oracle” adalah invalid XML, artinya kita yakin bahwa byte ke-4 IV F2 membuat byte ke-4 P1 menjadi 13.
Dengan mengetahui byte ke-4 IV dan byte ke-4 P1, kita bisa menghitung byte ke-4 hasil dekrip C1 adalah F2 XOR 13 = E1.
Mencari Byte ke-5
Mencari byte ke-5 prosedurnya tetap sama. Kita selalu mulai lagi dengan IV hasil prosedur “Find IV” di awal, yaitu IV yang membuat byte terakhir menjadi 01. Kemudian dari IV tersebut byte-5nya kita masking dengan 7 byte (00, 10, 20 – 70) untuk mencari byte ke-5 IV yang mentrigger error invalid XML.
Gambar di bawah ini adalah proses mencari byte ke-5 IV yang mentrigger error invalid XML. Ternyata hanya ada satu IV yang mentrigger error invalid XML, yaitu bila byte ke-5 bernilai 35.
Byte ke-5 IV, 35 ini membuat P1 menjadi salah satu dari 3 kandidat: 19, 1A atau 1D. Kita butuhkan “the oracle” untuk menentukan satu dari 3 kemungkinan kandidat itu. Caranya adalah kita meng-XOR-kan byte ke-5 IV (35) dengan 25, 26 dan 21 (untuk membuat byte ke-5 P1 menjadi 3C) kemudian melihat mana yang mentrigger error invalid XML.
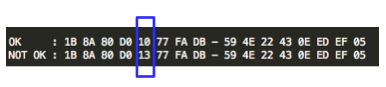 Perhatikan gambar di atas, ketika byte ke-5 IV menjadi 10 (=35 XOR 25) tidak mentrigger error invalid XML, namun ketika byte ke-5 IV menjadi 13 (=35 XOR 26) mentrigger error invalid XML. Dari 2 percobaan ini kita yakin bahwa byte ke-5 IV 13 membuat byte ke-5 P1 menjadi 3C.
Perhatikan gambar di atas, ketika byte ke-5 IV menjadi 10 (=35 XOR 25) tidak mentrigger error invalid XML, namun ketika byte ke-5 IV menjadi 13 (=35 XOR 26) mentrigger error invalid XML. Dari 2 percobaan ini kita yakin bahwa byte ke-5 IV 13 membuat byte ke-5 P1 menjadi 3C.
Dengan mengetahui byte ke-5 IV 13 membuat byte ke-5 P1 menjadi 3C, maka kita bisa menghitung byte ke-5 hasil dekrip C1 adalah 13 XOR 3C = 2F.
Mencari byte ke-6 s/d 15
Karena caranya sama, byte ke-6 sampai byte ke-15 saya tuliskan di bawah ini.
[spoiler title=”Proses mecari byte ke-6 s/d byte ke-15″]
********** Byte ke-6 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 67 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 57 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 47 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 37 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 27 FA DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 17 FA DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 07 FA DB – 59 4E 22 43 0E ED EF 05
####################
OK :1B 8A 80 D0 15 2B FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 3B FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 2A FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 3A FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 29 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 39 FA DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 28 FA DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 07 FA DB – 59 4E 22 43 0E ED EF 05
Byte ke-6 IV=7 –> byte ke-6 P1=13 –> byte ke-6 Decrypt(Ci)=14
********** Byte ke-7 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 EA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 DA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 CA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 BA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 AA DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 9A DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 8A DB – 59 4E 22 43 0E ED EF 05
####################
OK :1B 8A 80 D0 15 77 A6 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 B6 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 A7 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 B7 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 A4 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 B4 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 A5 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 B5 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 A2 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 B2 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 A3 DB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 B3 DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 9C DB – 59 4E 22 43 0E ED EF 05
Byte ke-7 IV=9C –> byte ke-7 P1=09 –> byte ke-7 Decrypt(Ci)=95
********** Byte ke-8 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA CB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA FB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA EB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA 9B – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA 8B – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA BB – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA AB – 59 4E 22 43 0E ED EF 05
####################
OK :1B 8A 80 D0 15 77 FA 8E – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA 8D – 59 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA 8A – 59 4E 22 43 0E ED EF 05
Byte ke-8 IV=8A –> byte ke-8 P1=3C sehingga byte ke-8 Decrypt(Ci)=B6
********** Byte ke-9 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 49 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 79 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 69 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 19 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 09 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 39 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 29 4E 22 43 0E ED EF 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 0C 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 0F 4E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 08 4E 22 43 0E ED EF 05
Byte ke-9 IV=8 –> byte ke-9 P1=3C sehingga byte ke-9 Decrypt(Ci)=34
********** Byte ke-10 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 5E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 6E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 7E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 0E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 1E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 2E 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 3E 22 43 0E ED EF 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 59 12 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 02 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 13 22 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 3C 22 43 0E ED EF 05
Byte ke-10 IV=3C –> byte ke-10 P1=13 –> byte ke-10 Decrypt(Ci)=2F
********** Byte ke-11 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 32 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 02 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 12 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 62 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 72 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 42 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 52 43 0E ED EF 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 7E 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 6E 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 7F 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 6F 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 7C 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 6C 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 7D 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 6D 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 7A 43 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 6A 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 45 43 0E ED EF 05
Byte ke-11 IV=45 –> byte ke-11 P1=09 –> byte ke-11 Decrypt(Ci)=4C
********** Byte ke-12 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 53 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 63 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 73 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 03 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 13 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 23 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 33 0E ED EF 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 1F 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 0F 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 1E 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 0E 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 1D 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 0D 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 1C 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 0C 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 1B 0E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 34 0E ED EF 05
Byte ke-12 IV=34 –> byte ke-12 P1=13 –> byte ke-12 Decrypt(Ci)=27
********** Byte ke-13 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 1E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 2E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 3E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 4E ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 5E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 6E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 7E ED EF 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 72 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 62 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 73 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 63 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 70 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 60 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 71 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 61 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 76 ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 66 ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 77 ED EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 58 ED EF 05
Byte ke-13 IV=58 –> byte ke-13 P1=13 –> byte ke-13 Decrypt(Ci)=4B
********** Byte ke-14 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E FD EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E CD EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E DD EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E AD EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E BD EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E 8D EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E 9D EF 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E B1 EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E A1 EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E B0 EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E A0 EF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E B3 EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E 9C EF 05
Byte ke-14 IV=9C –> byte ke-14 P1=09 –> byte ke-14 Decrypt(Ci)=95
********** Byte ke-15 **********
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED EF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED FF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED CF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED DF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED AF 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED BF 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED 8F 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED 9F 05
####################
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED B3 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED A3 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED B2 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED A2 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED B1 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED A1 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED B0 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED A0 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED B7 05
OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED A7 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED B6 05
NOT OK :1B 8A 80 D0 15 77 FA DB – 59 4E 22 43 0E ED 99 05
Byte ke-15 IV=99 –> byte ke-15 P1=13 –> byte ke-15 Decrypt(Ci)=8A
[/spoiler]
Setelah semua byte berhasil didekrip, kini hasil Dekrip blok C1 sudah lengkap. Bila kita kembalikan IV yang asli (bukan IV hasil prosedur “find IV”), kemudian kita XOR-kan antara hasil Dekrip C1 dan IV tersebut kita akan dapatkan plaintext yang benar.
Decrypting C2
Mendekrip C2 caranya sama dengan mendekrip C1, bedanya adalah kalau dulu kita pakai C0 dan C1 untuk mendekrip C1, kini kita pakai C1 dan C2 untuk mendekrip C2. Jadi prosedurnya tetap sama:
- “Find IV” untuk mencari IV yang membuat single byte padding
- Cari byte ke-X
Find IV Blok C2
Kita mulai prosedur pertama mencari IV yang membuat single byte padding. Input dari prosedur ini adalah dua blok, yaitu C1 (sebagai IV) dan C2 (sebagai blok yang akan didekrip).
Dengan cara yang sama seperti C1, kita akan mendapatkan 16 IV yang membuat P1 menjadi valid (valid padding dan valid XML).
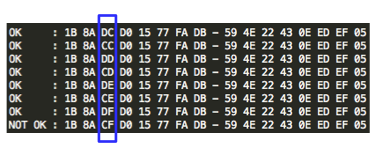
Kita hanya tahu 16 IV tersebut menghasilkan byte terakhir P1 antara 01 – 10, tapi kita tidak tahu pasti yang mana. Namun kita punya petunjuk bahwa ada satu IV yang bit ke-4nya berbeda sendiri dari 15 IV lainnya, dan IV yang berbeda sendiri itu adalah IV yang menghasilkan padding 10.
Kalau kita perhatikan ada 15 IV yang diawali dengan A, dan hanya ada satu IV yang diawali dengan B, yaitu B8. Dari situ kita bisa simpulkan bahwa byte terakhir IV B8 akan membuat byte terakhir P1 bernilai 10.
Karena tujuan kita adalah mencari IV yang membuat single byte padding, maka byte terakhir IV harus kita buat menjadi B8 XOR 11 = A9. Sekarang kita sudah dapatkan IV yang akan menjadi masukan bagi prosedur untuk mendekrip byte-byte dalam blok C2.
Mencari byte ke-16
Setelah mendapatkan IV yang membuat single byte padding, kita bisa dengan mudah menghitung byte ke-16 dari hasil Decrypt(c2) yaitu byte terakhir IV (A9) XOR 01 = A8.
Mencari byte ke-1 s/d ke-6
Dengan cara yang sama kita bisa mendekrip byte-byte mulai dari byte ke-1 sampai ke-15. Berikut ini adalah proses bagaimana mendekrip byte ke-1 s/d byte ke-6.
[spoiler title=”Proses mencari byte ke-1 s/d byte ke-6″]
********** Byte ke-1 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :39 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :09 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :19 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :69 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :79 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :49 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :59 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
####################
OK :75 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :65 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :74 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :64 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :77 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :67 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :76 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :66 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :71 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :61 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :70 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :60 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :4F D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
Byte ke-1 IV=4F –> byte ke-1 P1=13 –> byte ke-1 Decrypt(Ci)=5C
********** Byte ke-2 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 C0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 F0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 E0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 90 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 80 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 B0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 A0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
####################
OK :29 8C 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 9C 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 8D 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 9D 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 8E 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 9E 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 8F 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 9F 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 88 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 98 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 B7 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
Byte ke-2 IV=B7 –> byte ke-2 P1=13 –> byte ke-2 Decrypt(Ci)=A4
********** Byte ke-3 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 56 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 66 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 76 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 06 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 16 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 26 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 36 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
####################
OK :29 D0 1A 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 0A 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 1B 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 0B 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 18 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 08 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 19 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 09 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 1E 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 0E 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 1F 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 30 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
Byte ke-3 IV=30 –> byte ke-3 P1=13 –> byte ke-3 Decrypt(Ci)=23
********** Byte ke-4 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 71 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 41 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 51 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 21 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 31 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 01 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 11 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
####################
NOT OK :29 D0 46 7D 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 52 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
Byte ke-4 IV=52 –> byte ke-4 P1=13 –> byte ke-4 Decrypt(Ci)=41
********** Byte ke-5 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 6D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 5D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 4D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 3D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 2D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 1D 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 0D 75 99 47 – 76 17 A0 56 06 FF 46 A9
####################
OK :29 D0 46 61 21 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 31 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 20 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 30 75 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 23 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 0C 75 99 47 – 76 17 A0 56 06 FF 46 A9
Byte ke-5 IV=C –> byte ke-5 P1=09 –> byte ke-5 Decrypt(Ci)=5
********** Byte ke-6 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 65 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 55 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 45 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 35 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 25 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 15 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 05 99 47 – 76 17 A0 56 06 FF 46 A9
####################
OK :29 D0 46 61 7D 20 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 23 99 47 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 24 99 47 – 76 17 A0 56 06 FF 46 A9
Byte ke-6 IV=24 –> byte ke-6 P1=3C sehingga byte ke-6 Decrypt(Ci)=18
[/spoiler]
Mencari byte ke-7
Proses pencarian byte ke-7 akan saya bahas karena ternyata hasilnya agak sedikit berbeda dari contoh sebelumnya. Kali ini kita mendapatkan 3 IV yang mentrigger error invalid XML (contoh sebelumnya hanya 1 atau 2 IV), yaitu C9, F9, E9.
Seperti biasa kita tidak perlu memakai semua IV tersebut, kita pilih saja salah satu yaitu C9. Bila ditemukan 3 IV seperti ini maka ada 6 kemungkinan P1 di byte ke-7 yaitu: 0x06, 0x16, 0x26, 0x0C, 0x1C, 0x3C.
Bagaimana cara kita menentukan byte P1 yang mana dari 6 kandidat tersebut? Kita akan gunakan byte masking 3A, 2A, 1A, 30, 20 dan 00 untuk membantu menebak byte P1 yang benar.
Gambar di bawah ini adalah alur logika bagaimana menggunakan jawaban “the oracle” (valid/invalid XML) bisa membawa kita menuju byte P1 yang benar. Byte ke-7 IV (C9) akan kita XOR dengan byte masking tersebut kemudian melihat reaksi dari “the oracle”, apakah valid atau invalid XML. Bila ternyata invalid XML, kita XOR lagi dengan 2F sebagai ujian terakhir, bila reaksi “the oracle” adalah invalid XML, maka kita sudah berhasil menebak P1 dengan benar.
Setelah mengikuti alur logika di atas, diketahui bahwa invalid XML terjadi 2 kali di cabang 00 (ketika di XOR dengan 00). Dari hasil ini kita bisa menebak bahwa byte ke-7 P1 adalah 3C.
Dengan mengetahui bahwa byte ke-7 P1 adalah 3C dan byte ke-7 IV adalah C9, kita bisa menghitung byte ke-7 Decrypt(c2) adalah C9 XOR 3C = F5.
Mendekrip byte ke-8 s/d ke-15
Perlu diketahui bahwa hanya ada 3 kemungkinan ketika kita mencari IV yang membuat jadi invalid XML, yaitu 1 IV, 2 IV atau 3 IV. Pada byte ke-7 di atas kita mendapati bahwa terdapat 3 IV yang mentrigger error invalid XML, sedangkan pada contoh-contoh lain sebelumnya kita sudah menemukan contoh kasus 1 IV dan 2 IV.
Dengan cara yang sama, berikut adalah proses dekripsi byte ke-8 sampai byte ke-15.
[spoiler title=”Proses mencari byte ke-8 s/d byte ke-15″]
********** Byte ke-8 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 57 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 67 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 77 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 07 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 17 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 27 – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 37 – 76 17 A0 56 06 FF 46 A9
####################
OK :29 D0 46 61 7D 75 99 1B – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 0B – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 1A – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 0A – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 19 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 09 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 18 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 08 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 1F – 76 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 0F – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 20 – 76 17 A0 56 06 FF 46 A9
Byte ke-8 IV=20 –> byte ke-8 P1=09 –> byte ke-8 Decrypt(Ci)=29
********** Byte ke-9 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 66 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 56 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 46 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 36 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 26 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 16 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 06 17 A0 56 06 FF 46 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 2A 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 3A 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 2B 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 3B 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 28 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 38 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 29 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 39 17 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 16 17 A0 56 06 FF 46 A9
Byte ke-9 IV=16 –> byte ke-9 P1=13 –> byte ke-9 Decrypt(Ci)=5
********** Byte ke-10 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 07 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 37 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 27 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 57 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 47 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 77 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 67 A0 56 06 FF 46 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 76 12 A0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 11 A0 56 06 FF 46 A9
Byte ke-10 IV=11 –> byte ke-10 P1=3C sehingga byte ke-10 Decrypt(Ci)=2D
********** Byte ke-11 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 B0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 80 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 90 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 E0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 F0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 C0 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 D0 56 06 FF 46 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 76 17 FC 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 EC 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 FD 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 ED 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 FE 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 EE 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 FF 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 EF 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 F8 56 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 E8 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 C7 56 06 FF 46 A9
Byte ke-11 IV=C7 –> byte ke-11 P1=09 –> byte ke-11 Decrypt(Ci)=CE
********** Byte ke-12 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 46 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 76 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 66 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 16 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 06 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 36 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 26 06 FF 46 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 0A 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 1A 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 0B 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 1B 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 08 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 18 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 09 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 19 06 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 36 06 FF 46 A9
Byte ke-12 IV=36 –> byte ke-12 P1=13 –> byte ke-12 Decrypt(Ci)=25
********** Byte ke-13 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 16 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 26 FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 36 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 46 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 56 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 66 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 76 FF 46 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 1A FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 0A FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 1B FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 0B FF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 24 FF 46 A9
Byte ke-13 IV=24 –> byte ke-13 P1=13 –> byte ke-13 Decrypt(Ci)=37
********** Byte ke-14 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 EF 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 DF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 CF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 BF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 AF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 9F 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 8F 46 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FA 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 F9 46 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FE 46 A9
Byte ke-14 IV=FE –> byte ke-14 P1=3C sehingga byte ke-14 Decrypt(Ci)=C2
********** Byte ke-15 **********
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 46 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 56 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 66 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 76 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 06 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 16 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 26 A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 36 A9
####################
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 5A A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 4A A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 5B A9
OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 4B A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 58 A9
NOT OK :29 D0 46 61 7D 75 99 47 – 76 17 A0 56 06 FF 77 A9
Byte ke-15 IV=77 –> byte ke-15 P1=13 –> byte ke-15 Decrypt(Ci)=64
[/spoiler]
Kini kita sudah berhasil mendekrip c2 dari byte ke-1 sampai byte ke-16.
Gambar berikut adalah hasil dekripsi gabungan C1 dan C2
Selanjutnya dengan cara yang sama kita bisa melanjutkan untuk mendekrip C3, C4, C5 dan seterusnya.